Вдоль длинного тонкостенного круглого цилиндра радиуса течет ток какое давление
Содержание статьи
Вдоль длинного тонкостенного круглого цилиндра радиуса течет ток какое давление
Вдоль длинного тонкостенного круглого цилиндра радиуса течет ток какое давление
Разделы
Дополнительно
Задача по физике — 7555
Два длинных параллельных провода с пренебрежимо малым сопротивлением замкнуты с одного конца на некоторое сопротивление $R$, а с другого конца подключены к источнику постоянного напряжения. Расстояние между осями проводов в $eta = 20$ раз больше радиуса сечения каждого провода. При каком значении сопротивления $R$ результирующая сила взаимодействия между проводами обратится в нуль?
Задача по физике — 7556
Постоянный ток $I$ течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса Л. Такой же ток течет в противоположном направлении по тонкому проводнику, расположенному на «оси» первого проводника (точка О на рис.). Найти силу магнитного взаимодействия данных проводников в расчете на единицу их длины.
Задача по физике — 7557
По двум длинным тонким параллельным проводникам, вид которых показан на рис., текут постоянные токи $I_$ и $I_$. Расстояние между проводниками $a$, ширина правого проводника $b$. Имея в виду, что оба проводника лежат в одной плоскости, найти силу магнитного взаимодействия между ними в расчете на единицу их длины.
1>
Задача по физике — 7558
Система состоит из двух параллельных друг другу плоскостей с токами, которые создают между плоскостями однородное магнитное поле с индукцией $B$. Вне этой области магнитное поле отсутствует. Найти магнитную силу, действующую на единицу поверхности каждой плоскости.
Задача по физике — 7559
Проводящую плоскость с током поместили во внешнее однородное магнитное поле. В результате индукция магнитного Поля с одной стороны плоскости оказалась $B_$, а с другой стороны $B_$. Найти магнитную силу, действующую на единицу поверхности плоскости в случаях, показанных на рис. Выяснить, куда направлен ток в плоскости в каждом случае.
1>
Задача по физике — 7560
В электромагнитном насосе для перекачки расплавленного металла участок трубы с металлом находится в однородном магнитном поле с индукцией $B$ (рис.). Через этот участок трубы в перпендикулярном к вектору $vec$ и оси трубы направлении пропускают ток $I$. Найти избыточное давление, создаваемое насосом при $vec = 0,10 Т, I = 100 А$ и $a = 2,0 см$.
Задача по физике — 7561
Вдоль длинного тонкостенного круглого цилиндра радиуса $R$ течет ток $I$. Какое давление испытывают стенки цилиндра?
Задача по физике — 7562
Какое давление испытывает боковая поверхность длинного прямого соленоида, содержащего $n$ витков на единицу длины, когда по нему течет ток $I$?
Задача по физике — 7563
Ток $I$ течет по длинному однослойному соленоиду, радиус сечения которого равен $R$. Число витков на единицу длины соленоида $n$. Найти предельную силу тока, при которой может наступить разрыв обмотки, если предельная нагрузка на разрыв проволоки обмотки равна $F_$.
пр>
Задача по физике — 7564
Плоский конденсатор, площадь каждой пластинки которого $S$ и расстояние между ними $d$, поместили в поток проводящей жидкости с удельным сопротивлением $rho$. Жидкость движется с постоянной скоростью $v$ параллельно пластинам. Система находится в, однородном магнитном поле с индукцией $B$, причем вектор $vec$ параллелей пластинам и перпендикулярен к направлению потока. Пластины конденсатора замкнули на внешнее сопротивление $R$. Какая мощность выделяется на этом сопротивлении? При каком значении $R$ выделяемая мощность будет максимальной? Чему равна последняя?
Задача по физике — 7565
Вдоль медного прямого проводника круглого сечения радиуса $R = 5,0 мм$ течет ток $I = 50 А$. Найти разность потенциалов между осью проводника и его поверхностью. Концентрация электронов проводимости у меди $n = 0,9 cdot 10^ см^$.
23>
Задача по физике — 7566
При измерении эффекта Холла в натриевом проводнике напряженность поперечного поля оказалась $E = 5,0 мкВ/см$ при плотности тока $j = 200 А/см^$ и индукции магнитного поля $B = 1,00 Т$. Найти концентрацию электронов проводимости и ее отношение к концентрации атомов в данном проводнике.
2>
Задача по физике — 7567
Найти подвижность электронов проводимости в медном проводнике, если при измерении эффекта Холла в магнитном поле с индукцией $B = 100 мТ$ напряженность поперечного электрического поля у данного проводника оказалась в $eta = 3,1 cdot 10^$ раз меньше напряженности продольного электрического поля.
3>
Задача по физике — 7568
Небольшой виток с током находится на расстоянии $r$ от длинного прямого проводника с током $I$. Магнитный момент витка равен $vec
_$. Найти модуль и направление вектора силы, действующей на виток, если вектор $vec
_$:
а) параллелен прямому проводнику,
б) направлен по радиус-вектору $vec$;
в) совпадает по направлению с магнитным полем тока $I$ в месте расположения витка.
Задача по физике — 7569
Небольшая катушка с током, имеющая магнитный момент $vec
_$, находится на оси кругового витка радиуса $R$, по которому течет ток $I$. Найти модуль вектора силы, действующей на катушку, если ее расстояние от центра витка равно $x$, а вектор $vec
_$ совпадает по направлению с осью витка.
Источник
Вдоль длинного тонкостенного круглого цилиндра радиуса течет ток какое давление
Разделы
Дополнительно
Задача по физике — 7556
Постоянный ток $I$ течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса Л. Такой же ток течет в противоположном направлении по тонкому проводнику, расположенному на «оси» первого проводника (точка О на рис.). Найти силу магнитного взаимодействия данных проводников в расчете на единицу их длины.
Задача по физике — 7557
По двум длинным тонким параллельным проводникам, вид которых показан на рис., текут постоянные токи $I_$ и $I_$. Расстояние между проводниками $a$, ширина правого проводника $b$. Имея в виду, что оба проводника лежат в одной плоскости, найти силу магнитного взаимодействия между ними в расчете на единицу их длины.
1>
Задача по физике — 7558
Система состоит из двух параллельных друг другу плоскостей с токами, которые создают между плоскостями однородное магнитное поле с индукцией $B$. Вне этой области магнитное поле отсутствует. Найти магнитную силу, действующую на единицу поверхности каждой плоскости.
Задача по физике — 7559
Проводящую плоскость с током поместили во внешнее однородное магнитное поле. В результате индукция магнитного Поля с одной стороны плоскости оказалась $B_$, а с другой стороны $B_$. Найти магнитную силу, действующую на единицу поверхности плоскости в случаях, показанных на рис. Выяснить, куда направлен ток в плоскости в каждом случае.
1>
Задача по физике — 7560
В электромагнитном насосе для перекачки расплавленного металла участок трубы с металлом находится в однородном магнитном поле с индукцией $B$ (рис.). Через этот участок трубы в перпендикулярном к вектору $vec$ и оси трубы направлении пропускают ток $I$. Найти избыточное давление, создаваемое насосом при $vec = 0,10 Т, I = 100 А$ и $a = 2,0 см$.
Задача по физике — 7561
Вдоль длинного тонкостенного круглого цилиндра радиуса $R$ течет ток $I$. Какое давление испытывают стенки цилиндра?
Задача по физике — 7562
Какое давление испытывает боковая поверхность длинного прямого соленоида, содержащего $n$ витков на единицу длины, когда по нему течет ток $I$?
Задача по физике — 7563
Ток $I$ течет по длинному однослойному соленоиду, радиус сечения которого равен $R$. Число витков на единицу длины соленоида $n$. Найти предельную силу тока, при которой может наступить разрыв обмотки, если предельная нагрузка на разрыв проволоки обмотки равна $F_$.
пр>
Задача по физике — 7564
Плоский конденсатор, площадь каждой пластинки которого $S$ и расстояние между ними $d$, поместили в поток проводящей жидкости с удельным сопротивлением $rho$. Жидкость движется с постоянной скоростью $v$ параллельно пластинам. Система находится в, однородном магнитном поле с индукцией $B$, причем вектор $vec$ параллелей пластинам и перпендикулярен к направлению потока. Пластины конденсатора замкнули на внешнее сопротивление $R$. Какая мощность выделяется на этом сопротивлении? При каком значении $R$ выделяемая мощность будет максимальной? Чему равна последняя?
Задача по физике — 7565
Вдоль медного прямого проводника круглого сечения радиуса $R = 5,0 мм$ течет ток $I = 50 А$. Найти разность потенциалов между осью проводника и его поверхностью. Концентрация электронов проводимости у меди $n = 0,9 cdot 10^ см^$.
23>
Задача по физике — 7566
При измерении эффекта Холла в натриевом проводнике напряженность поперечного поля оказалась $E = 5,0 мкВ/см$ при плотности тока $j = 200 А/см^$ и индукции магнитного поля $B = 1,00 Т$. Найти концентрацию электронов проводимости и ее отношение к концентрации атомов в данном проводнике.
2>
Задача по физике — 7567
Найти подвижность электронов проводимости в медном проводнике, если при измерении эффекта Холла в магнитном поле с индукцией $B = 100 мТ$ напряженность поперечного электрического поля у данного проводника оказалась в $eta = 3,1 cdot 10^$ раз меньше напряженности продольного электрического поля.
3>
Задача по физике — 7568
Небольшой виток с током находится на расстоянии $r$ от длинного прямого проводника с током $I$. Магнитный момент витка равен $vec
_$. Найти модуль и направление вектора силы, действующей на виток, если вектор $vec
_$:
а) параллелен прямому проводнику,
б) направлен по радиус-вектору $vec$;
в) совпадает по направлению с магнитным полем тока $I$ в месте расположения витка.
Задача по физике — 7569
Небольшая катушка с током, имеющая магнитный момент $vec
_$, находится на оси кругового витка радиуса $R$, по которому течет ток $I$. Найти модуль вектора силы, действующей на катушку, если ее расстояние от центра витка равно $x$, а вектор $vec
_$ совпадает по направлению с осью витка.
Задача по физике — 7570
Найти силу взаимодействия двух катушек с магнитными моментами $p_ = 4,0 мА cdot м^$ и $p_ = 6,0 мА cdot м^$, если их оси лежат на одной прямой и расстояние между катушками, равное $l = 20 см$, значительно превышает их линейные размеры.
1m>
Источник
Вдоль длинного тонкостенного круглого цилиндра радиуса течет ток какое давление
Разделы
Дополнительно
Задача по физике — 7526
Очень длинный проводник с током $I = 5,0 А$ изогнут в форме прямого угла. Найти индукцию магнитного поля в точке, которая отстоит от плоскости проводника на $l = 35 см$ и находится на перпендикуляре к проводникам, проходящем через точку изгиба.
Задача по физике — 7527
Найти индукцию магнитного поля в точке О, если проводник с током $I = 8,0 А$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника $R = 100 мм$, прямолинейные участки проводника очень длинные.
Задача по физике — 7528
Определить модуль и направление вектора $vec$ магнитного поля:
а) безграничной плоскости, По которой течет ток с линейной плотностью $vec$, одинаковой во всех точках плоскости;
б) двух параллельных безграничных плоскостей, по которым текут токи с линейными плотностями $vec$ и $- vec$, одинаковыми во всех точках каждой плоскости.
Задача по физике — 7529
Однородный ток плотности $j$ течет внутри неограниченной пластины толщины $2d$ параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния $x$ от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице.
Задача по физике — 7530
Постоянный ток $I$ течет по длинному прямому проводу. Из точки О (рис.) он растекается радиально-симметрично по безграничной проводящей плоскости, перпендикулярной к проводу. Найти индукцию магнитного поля во всех точках пространства.
Задача по физике — 7531
Имеется круговой виток с током $I$. Найти интеграл $int vec d vec$ вдоль оси витка в пределах от $ — infty$ до $+ infty$. Объяснить полученный результат.
Задача по физике — 7532
По круглому однородному прямому проводу, радиус сечения которого $R$, течет постоянный ток плотности $vec$. Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус-вектором $vec$. Магнитную проницаемость всюду считать равной единице.
Задача по физике — 7533
Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние $vec$. По проводу течет постоянный ток плотности $vec$. Найти вектор индукции магнитного поля внутри полости. Рассмотреть, в частности, случай $vec = 0$.
Задача по физике — 7534
Найти плотность тока как функцию расстояния $r$ от оси аксиально-симметричного параллельного потока электронов, если, индукция магнитного поля внутри потока зависит от $r$ как $B = br^$, где $b$ и $alpha$ — положительные постоянные.
Задача по физике — 7535
Однослойная катушка (соленоид) имеет длину $l$ и радиус сечения $R$. Число витков на единицу длины $n$. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока $I$.
Задача по физике — 7536
Очень длинный прямой соленоид имеет радиус сечения $R$ и $n$ витков на единицу длины. По соленоиду течет постоянный ток $I$. Пусть $x$ — расстояние, отсчитываемое вдоль оси соленоида от его торца. Найти:
а) индукцию магнитного поля на оси как функцию $x$; изобразить примерный график зависимости индукции $B$ от отношения $x/R$;
б) расстояние $x_$ до точки на оси, в которой индукция поля отличается от индукции в глубине соленоида на $eta = 1$%.
Задача по физике — 7537
Обмоткой очень длинного прямого соленоида с радиусом сечения $R = 2,5 см$ служит тонкая лента-проводник шириной $h = 2,0 см$, намотанная в один слой практически вплотную. По ленте течет постоянный ток $I = 5,0 А$. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния $r$ от его оси.
Задача по физике — 7538
На деревянный тороид малого поперечного сечения намотано равномерно $N = 2,5 cdot 10^$ витков провода, по которому течет ток $I$. Найти отношение $eta$ индукции магнитного поля внутри тороида к индукции магнитного поля в центре тороида.
3>
Задача по физике — 7539
Постоянный ток $I = 10 А$ течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины.
Задача по физике — 7540
Имеется очень длинный прямой соленоид с током $I$. Площадь поперечного сечения соленоида равна $S$, число витков на единицу длины — $n$. Найти поток вектора $vec$ через торец соленоида.
Источник
Источник
Экзаменационные задачи по дисциплине «Теоретические основы электротехники», 3-я часть – электромагнитное поле (с ответами), страница 3
Таким образом, скалярные магнитные потенциалы определены:
;
;
.
Теперь можно определить напряженность магнитного поля в каждой области:
1) Внутри трубы
, т.е. внутри трубы магнитное поле однородно (при однородном внешнем поле с напряженностью Н0).
2) В стенке трубы
;
;
3) Вне трубы
;
.
Коэффициент экранирования
.
Если , то .
Билет №12. Определить силу, действующую на частицу с зарядом Q = 1,6 ×10-19Кл, движущуюся в магнитном поле с индукцией В = 1,5Тл. Частица движется со скоростью v = 2,5 ×106 м/с под углом a = 45° к направлению вектора магнитной индукции.
Решение.
, Н.
Так как заряженная частица движется под углом к направлению магнитного поля, то ее траектория представляет собой винтовую линию. При движении заряженной частицы под прямым углом к направлению магнитного поля ее траектория была бы окружностью в плоскости, нормальной к магнитному полю.
Билет №13. Плоскость рамки составляет угол a = 30 ° с направлением однородного магнитного поля в воздухе с индукцией B = 0,1 Тл (рис.1). Площадь рамки S = 100см2. Число витков w = 50, ток в рамке I = 4А. Определить вращающий момент рамки.
Рис.1
Решение. Сила, действующая на сторону рамки,
f = ВIlw,
где l — длина рамки.
Вращающий момент рамки
Мвр = f, где — ширина рамки.
.
Наибольший вращающий момент у рамки будет при = 0, когда она займет вертикальное положение, наименьший вращающий момент, равный нулю, будет при горизонтальном положении рамки. Рамка с постоянным током стремится занять такое положение, при котором ее пронизывает максимальный магнитный поток.
Билет №14. Расстояние между проводами d = 10 см (рис.1). Токи в проводах I1 = 1000А, I2 = 500А направлены в одну сторону. Длина проводов 1м. Определить магнитную силу взаимодействия f.
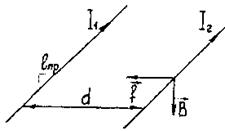
Рис.1
Решение.
=1 Н.
Провода притягиваются.
Билет №15. По двум параллельным проводам двухпроводной линии протекают равные по величине, но противоположно направленные токи I1 = I2 = 400А. Расстояние между осями проводов d = 0,3м. Найти величину и направление магнитной силы, действующей на 1 км длины каждого провода.
Решение:
Н.
Эти силы отталкивают провода.
Билет №16. Два длинных провода с пренебрежимо малым сопротивлением замкнуты с одного конца на сопротивление R, а с другого конца подключены к источнику постоянного напряжения (рис.1). Радиус сечения каждого провода r0 в 20 раз меньше расстояния между осями проводов . При каком значении сопротивления R результирующая сила взаимодействия проводов обратится в нуль?

Рис.1
Решение. На каждом из проводов (протекает по ним ток или нет) при подключении их к источнику напряжения имеются свободные заряды. Линейная плотность зарядов . Поэтому кроме магнитной силы fм необходимо учесть и электрическую fэ. Электрическая сила fэ, действующая на единицу длины провода со стороны другого провода
fэ = tЕ.
Величина Е равна
, поэтому
.
Магнитная сила fм на единицу длины провода
, где I — сила тока в проводе.
Обе силы — электрическая и магнитная — направлены в противоположные стороны: электрическая сила обусловливает притяжение проводов, магнитная — их отталкивание. Отношение сил
.
Билет №17. Вдоль длинного тонкостенного круглого цилиндра радиуса R течет ток I. Какое давление испытывают стенки цилиндра?
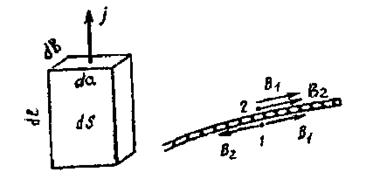
а) б)
Рис.1
Решение. Рассмотрим поверхностный элемент тока I’dS, где I’ — линейная плотность тока (I’ = , где l — длина цилиндра), dS — элемент поверхности цилиндра (рис.1). При этом
.
Смысл входящих сюда величин пояснен на рис.1,а. В векторном виде
.
Сила Ампера, действующая на поверхностный ток с учетом последнего выражения,
, где — магнитная индукция поля в месте нахождения рассматриваемого элемента тока от всех других элементов тока, исключая данный.
Определим величину . Пусть В2 — магнитная индукция, создаваемая самим элементом тока. Для магнитного поля плоскости с током мы получили
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Источник
Вдоль длинного тонкостенного круглого цилиндра радиуса r 5 см течет ток
Вдоль длинного тонкостенного круглого цилиндра радиуса r 5 см течет ток
Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.
Поле бесконечной однородно заряженной плоскости
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:
где d q — заряд, сосредоточенный на площади d S; d S — физически бесконечно малый участок поверхности.
Пусть σ во всех точках плоскости S одинакова. Заряд q — положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).
| Рис. 2.11 | Рис. 2.12 |
Применим теорему Остроградского-Гаусса. Поток ФЕчерез боковую часть поверхности цилиндра равен нулю, т.к . Дляоснования цилиндра
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:
Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского-Гаусса получим:
откуда видно, что напряженность поля плоскости S равна:
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости
Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей .
Тогда внутри плоскостей
Вне плоскостей напряженность поля
Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
Механические силы, действующие между заряженными телами, называют пондермоторными.
Тогда сила притяжения между пластинами конденсатора:
где S — площадь обкладок конденсатора. Т.к. , то
Это формула для расчета пондермоторной силы.
Поле заряженного бесконечно длинного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью , где d q — заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r.
Следовательно, поток вектора через рассматриваемую поверхность, равен
При на поверхности будет заряд По теореме Остроградского-Гаусса , отсюда
Если , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
Если уменьшать радиус цилиндра R (при ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.
Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
Внутри меньшего и вне большего цилиндров поле будет отсутствовать (рис. 2.16) .
В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:
Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).
Поле заряженного пустотелого шара
Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, — в любой точке проходит через центр шара. ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара — сферу радиуса r (рис. 2.17).
Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
откуда поле вне сферы:
Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов:
Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
Поле объемного заряженного шара
Для поля вне шара радиусом R (рис. 2.18) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:
Но внутри шара при сферическая поверхность будет содержать в себе заряд, равный
где ρ — объемная плотность заряда, равная: ; — объем шара. Тогда по теореме Остроградского-Гаусса запишем:
Источник
Вдоль длинного тонкостенного круглого цилиндра радиуса r 5 см течет ток
2.225 Точечный заряд движется со скоростью v = 900 м/с. В некоторый момент в точке Р напряженность поля этого заряда Е = 600 В/м, а между векторами Е и v угол а = 30°. Найти индукцию В магнитного поля данного заряда в точке Р в этот момент.
→ Перейти к решению
2.226 По круговому витку радиуса R = 100 мм из тонкого провода циркулирует ток I = 1,00 А. Найти магнитную индукцию: а) в центре витка; б) на оси витка на расстоянии x = 100 мм от его центра.
→ Перейти к решению
2.227 Кольцо радиуса R = 50 мм из тонкого провода согнули по диаметру под прямым углом. Найти магнитную индукцию в центре кривизны полуколец при токе I = 2,25 А.
→ Перейти к решению
2.228 Ток I течет по плоскому контуру, показанному на рис. , где r = r0(1 + ф). Найти магнитную индукцию В в точке О.
→ Перейти к решению
2.229 Ток I течет по тонкому проводнику, который имеет вид правильного n-угольника, вписанного в окружность радиуса R. Найти магнитную индукцию в центре данного контура. Исследовать случай n -> оо.
→ Перейти к решению
2.230 Найти магнитную индукцию в центре контура, имеющего вид прямоугольника, если его диагональ d = 16 см, угол между диагоналями ф = 30° и ток I = 5,0 А.
→ Перейти к решению
2.231 Ток I = 5,0 А течет по тонкому замкнутому проводнику (рис. ). Радиус изогнутой части R = 120 мм, угол 2ф = 90°. Найти магнитную индукцию в точке О.
→ Перейти к решению
2.232 Найти индукцию магнитного поля в точке О контура с током I, который показан: а) на рис. ; радиусы a и b, а также угол ф известны; б) на рис. ; радиус a и сторона b известны.
→ Перейти к решению
2.233 Ток I течет вдоль длинной тонкостенной трубы радиуса R, имеющей по всей длине продольную прорезь ширины h. Найти индукцию магнитного поля внутри трубы, если h
Источник
Закон Био-Савара. Теорема о циркуляции для магнитного поля
16. По круговоаму витку радиуса R циркулирует ток I. Определить индукцию магнитного поля на оси витка в зависимости от расстояния х от его центра. Построить график этой зависимости. Исследовать предельные случаи x >R.
Решение
Вследствие осевой симметрии полный вектор индукции на оси Ох направлен вдоль этой оси.
По закону Био-Савара вклад в проекцию вектора индукции магнитного поля на ось Ох от элемента длины кольца dl, расположенного в точке А (на рисунке) составляет dBх=(m/4p)(Idl/r 2 )sina. Вектор лежит в плоскости, проходящей через ось Ох и точку А и перпендикулярен . Величина sina=R/r одна и та же для всех точек кольца. Полная величина магнитной индукции составляет
B(x)=(m/2)IR 2 /r 3 =(m/2)IR 2 /(R 2 +x 2 ) 3/2
При x >R B(x)=(m/2)IR 2 /x 3 .
17. Длинный проводник с током I = 3А изогнут в форме прямого угла. Определить индукцию магнитного поля в точке, лежащей на биссектрисе угла на расстоянии L = 10 см от вершины угла О.
Решение
Сначала найдем индукцию магнитного поля, создаваемого прямолинейным отрезком длиной D проводника с током I.Пусть R — длина перпендикуляра, проведенного на отрезок из точки наблюдения, r — расстояние от точки наблюдения до элемента отрезка длиной dl, da=dl/r -угол, под которым виден элемент отрезка dl из точки наблюдения. Пусть также a — угол между перпендикуляком к отрезку и прямой, проведенной из точки наблюдения к элементу отрезка, тогда R=rcosa. По закону Био-Савара вклад в индукцию магнитного поля элемента отрезка dl составит
После интегрирования по длине отрезка получается
Здесь a1и a2 — углы между перпендикуляком к отрезку и прямыми, проведенными из точки наблюдения к концам отрезка.
Индукция магнитного поля в точке, лежащей на биссектрисе угла на расстоянии L от вершины угла, создается двумя лучами, являющимися сторонами угла. Вследствие симметрии относительно биссектрисы угла вклад в индукцию каждого из лучей одинаков.
Для одного луча a1=p/2, a2=-p/4, R=Lcos(p/4), и
= 2 10 -6 (3/0.1)0.42=2.48 10 -5 Тл
18. По длинному прямому цилиндрическому проводу радиуса R течет ток с постоянной плотностью j. Определить индукцию магнитного поля как функцию расстояния r от оси провода и построить график этой зависимости.
Решение
Индукция магнитного поля обладает в этой задаче осевой симметрией и вследствие однородности вдоль проводника от координаты вдоль проводника не зависит. Силовые линии поля — концентрические окружности с общим центром на оси проводника. Вектор индукции направлен по касательным к этим окружностям. Эти окружности следует выбрать в качестве замкнутых контуров для применения теоремы о циркуляции:
где I=pR 2 j — полный ток в проводнике. Отсюда следует
19. По оси длинного тонкостенного проводящего цилиндра радиуса R натянут провод. По цилиндру и проводу течет постоянный ток силы I, направление тока в проводе и цилиндре противоположны. Определить индукцию магнитного поля в зависимости от расстояния r от провода и построить график этой зависимости.
Решение
Индукция магнитного поля обладает в этой задаче осевой симметрией и вследствие однородности вдоль проводника от координаты вдоль проводника не зависит. Силовые линии поля — концентрические окружности с общим центром на оси проводника. Вектор индукции направлен по касательным к этим окружностям. Эти окружности следует выбрать в качестве замкнутых контуров для применения теоремы о циркуляции:
20. Тороидальная однослойная катушка содержит N витков плотно намотанного провода, по которому течет ток I.Внутренний радиус тора R1,внешний — R2. Определить индукцию магнитного поля внутри и вне тора на расстоянии r от его оси.
Решение
Тор представляет собой поверхнсть вращения окружности радиуса R = (R2 — R1)/2 вокруг оси, расположенной вне окружности. Полагая провод тонким по сравнению с радиусом тора, можно считать, что линии тока лежат в меридианальных плоскостях, т.е. в плоскостях, проходящих через ось вращения. При этом предположении при повороте тора с намотанным на него проводом с током вокруг оси он совмещается сам с собою. То же относится и к силовым линиям индукции магнитного поля тока. Поэтому силовые линии поля представляют собой концентрические окружности с центрами на оси вращения. Циркуляция вектора индукции магнитного поля вдоль каждой такой окружности радиуса r равна 2prB(r) Полный ток, пронизывающий площадь, ограниченную этой окружностью, равен NI, если окружностьпроходит внутри тора, и равен нулю, если она проходит вне тора.Таким образом, индукция поля отлична от нуля только внутри тора, т.е при R1
21. Соленоид представляет собой полый цилиндр радиуса R и длины L, на поверхность которого плотно намотан в один слой тонкий провод. Отношение числа витков провода в обмотке соленоида к его длине составляет n. Определить индукцию магнитного поля внутри и вне соленоида, если по его обмотке течет ток I. Провести оценки для следующих величин: R=1 см, L=50 см, n=15 витков/см, I=1 А.
Решение
Соленоид можно представить себе как предельный случай тора очень большого радиуса вращения, но фиксированного радиуса цилиндра R при увеличении числа витков обмотки, но фиксированном отношении n числа витков к длине окружности вращения. Индукция магнитного поля внутри соленоида составляет B= mnI, вне соленоида B=0.
Давление магнитного поля p=B 2 /2m. Сила давления, действующая на боковую поверхность соленоида, площадь которой S=2pRL составит
B=1.256 10 -6 15 1=1.88 10 -5 Тл p=1.41 10 -4 Н/м 2 F=4.44 10 -6 Н
Источник
Задачники FIZMATBANK.RU
Вход на сайт
Навигация по сайту
Статистика решений
| Тип решения | Кол-во |
| подробное решение | 61157 |
| краткое решение | 7600 |
| указания как решать | 1387 |
| ответ (символьный) | 4710 |
| ответ (численный) | 2385 |
| нет ответа/решения | 3604 |
| ВСЕГО | 80843 |
Задачи по общей физике
Иродов И.Е. , 2010 год
Задачник по физике
Чертов , 2009 год
Физика. Задачи с ответами и решениями
Черноуцан А.И. , 2009 год
Сборник задач по общему курсу ФИЗИКИ
Волькенштейн В.С. , 2008 год
Сборник задач по курсу физики
Трофимова Т.И. , 2008 год
Сборник вопросов и задач по физике. 10-11 класс.
Гольдфарб Н.И. , 1982 год
Задачи по общей физике
Иродов И.Е. , 1979 год
Сборник задач по общему курсу физики
Волькенштейн В.С. , 1997 год
Сборник задач по физике
Кашина С.И., Сезонов Ю.И. , 2010 год
Физика. Задачи для поступающих в ВУЗы
Бендриков Г.А.,Буховцев Б.Б.,Керженцев В.В.,Мякишев Г.Я. , 2005 год
Физика. Методические указания и контрольные задания.
Чертов А.Г. , 1987 год
Задачи физических олимпиад
Кембровский Г.С. , 2000 год
Задачник Кванта
коллектив авторов , 2010 год
Сборник задач по физике
Козел С.М., Баканина Л.П., Белонучкин В.Е. и др. , 1971 год
Сборник задач по элементарной физике
Буховцев Б.Б., Кривченков В.Д., Мякишев Г.Я., Сараева И.М. , 1974 год
Источник
Источник