Какой должен быть градиент давления
Содержание статьи
1. . () 3-4 2. (/), , . , , , 1,0 2 ( ). 1,0-1,5 2, 1,5 2. 2. . . ( ) , . ) . — , . . , . , , : — 12 => 1,13 2, — 11 => 0,95 2, — 10 => 0,8 2, — 9 => 0,65 2, — 8 => 0,5 2. , . , . , — , .
) . . , ( ). , — . . Otto . . 1. . . , , , . , , , , , . . — , . 4,56 /, 83 . ., 50 .. 2. . , . . , , , , .. , . (, ), — — / . 90% . . . 3. . — (, ) (, ), , , . , , /, , , , , . , . , , — , , . , , ! ) . (V1) (V2), : ΔP = 4(V22-V12). (V1<1,3 /), , (V1222), : ΔP = 4V22. , , . (ΔPm) : ΔPm=4(V12+V22+V12+…+Vn2)/n. . . ( , ) , , , , . , , ( , V1 ). , , .
) , . , , . . — . . . , . , . 1. . , , , -. , , . , , V1. 2. . , , . , , , . 20 6%, α 40 — 24%, 60 — 50%. , , , . , , .. . 3. . , (ΔP = 4V22) V1 . , , . V1, ΔP = 4(V22-V12). 4. . , , . , , . , . , , . , : , .
5. (Peak-to-Peak) . . , , , , . , .. (Peak-to-Peak) . () , ; . , , . , 20 .. 6. . RR, , . , R-R ( ), .
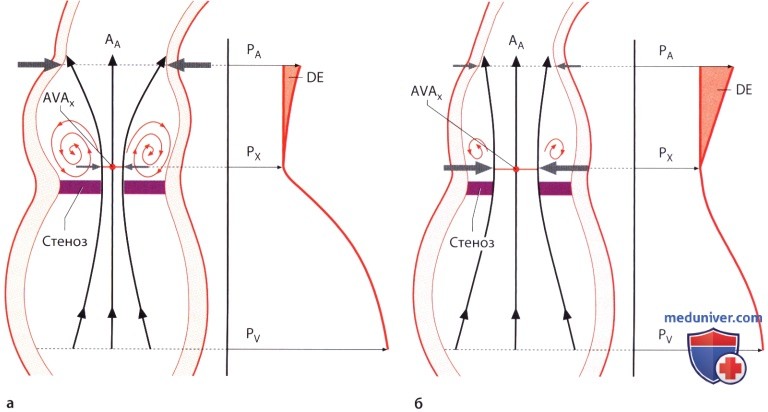
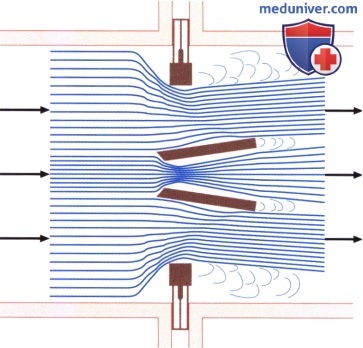
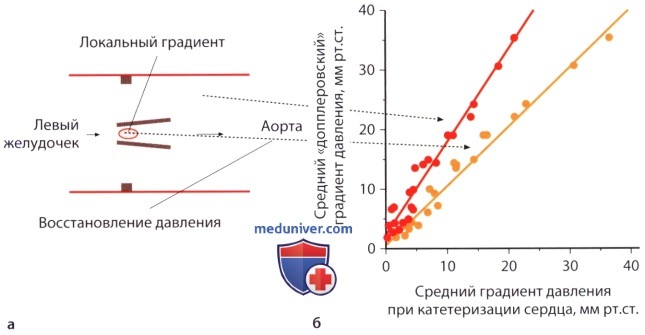
— (AVAX) (AA) (DE) . — (AVAX) (AA) , (DE). 7. . ( pressure-recovery phenomenon) — , . . . , (.. vena contracta). , . , . , . , . . , . 8. . , , , vena contracta, , , .. , , .. . , , , (.. ). , , . , , . Baumgartner . 7 23 20 .. , , , 20 .. , 3 . ( 1,7 ) 75 .. (AVAX) A. , , AVAX A: / = 2 (AVAX/AA — AVAX2/AA2. , : — (AVAX 0,5 2) 4 ( 12,6 2) 8%. — (AVAX 1,2 2) ( 2,5 , 4,9 2) 37%. , . , , . ) . , , . : . . , 50 .., (84%), (66%) (AVAX2). . . , . , . , , . 1. . ( 30 70). , . , , , . . . , , , . , , , . , , . . , . — . , , — , . , .
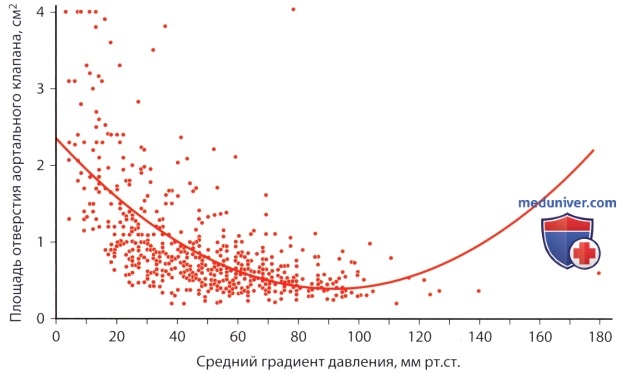
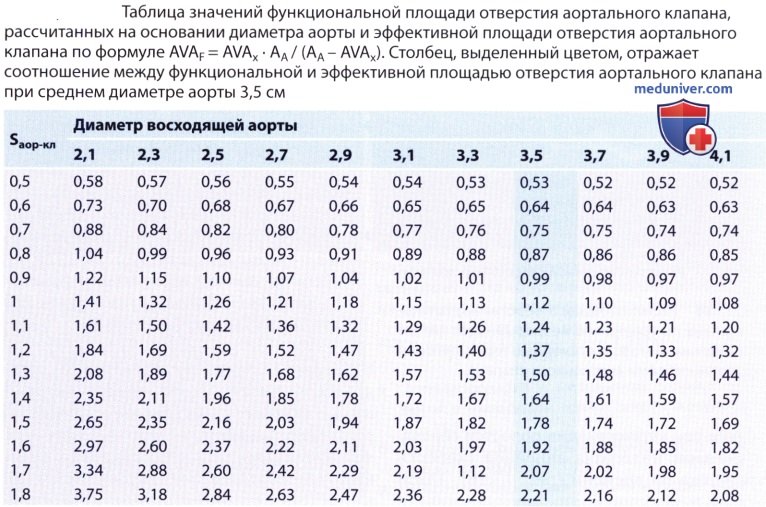
— : : V1 =110 /. — : : D = 2,4 . — : V2 = 400 /. 2. . , , Q . , , () (V). 3. . , , , (D) A1 = π(D/2)2. , . ; 3-5 . (V1) . 0,5 . , V2 c . (AVA = 2) : A2 = A1 * (V1/V2). , . . 5-8%, 0,15 2, , . , . , 2 (, 22 20 ) 21% (, 1,0 2 0,8 2). : , , , . , , . , , . , . 4. . (AVAX) , . ( ), .. , (AA). (AVAF), , : AVAF = (AVAX * AA/(AA -AVAX). , , : — AVAX, 1,0 2, , 2,5 ( AA 5 2), 1,25 2 — AVAX, 0,5 2, 3,6 ( AA 10 2) 0,53 2. . , 175 : Schobel .: 3,70,8 ; Baumgartner .: 3,10,6 ; Treat .: 3,550,4 . , , , . , . , , , . , , , . ) : 1. (valvular resistance). , , . R , : R[ * * -5] = 1333 * 4((Vmax)2/SLVOT)*VLVOT, LVOT — (left ventricular outflow tract). , , . , , , — , ( , , ). 2. . (SWL , stroke work loss) , . SWL , : SWL(%) = ΔP/PLVSP, PLVSP — . , 25%, . , SWL, , . 3. . V1/V2 . , . V1/V2 0,25 . , , , , . 4. , , . (FS — Fractional Shortening) , ΔP=4V2. , , -. . Karpuz . 0,8 (97%) (78%) (AVA≤0,53 2/2) Otto ., 382 , , . FS, , , , , FS, , , .. . , . , Antonini-Canterin . , , , . , . , , , , .
5. . () ()-/ , , , , , . /, 0,3, ; . , , / . ) -. , , , , , , , . V1/V2. 1. . [ ]. — , . 2. . — , . 3. V1/V2. , V1/V2. 4. (V2) . , V2 . 5. . , , , (, ), (), . — ,— » « : . : 29.1.2021 |
Источник
—
—, . , , , , — , ().
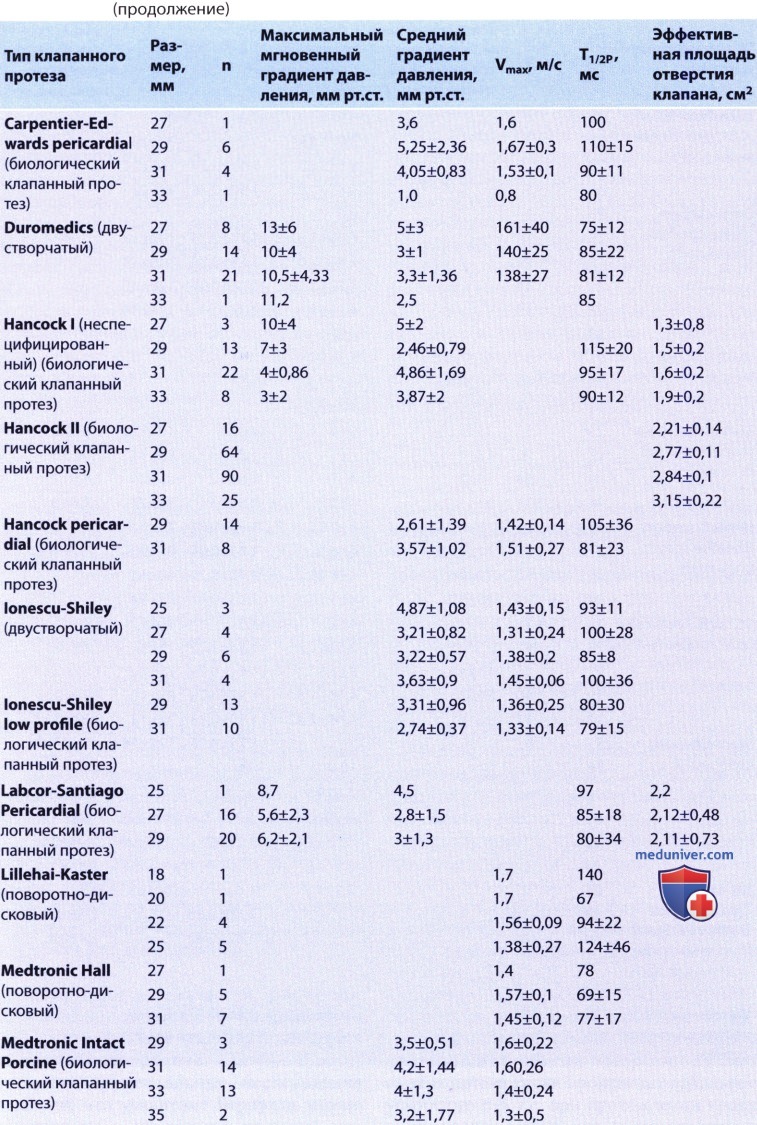
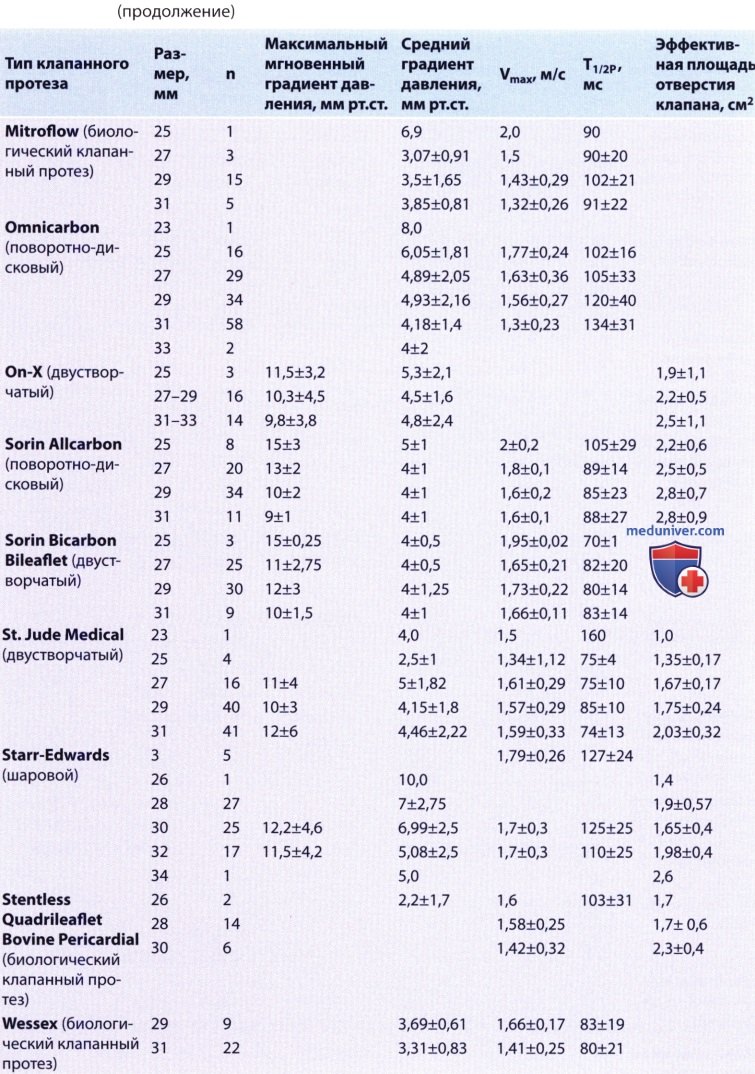
) : 1. . , , 20, . , , , , . — . , , , . . , , . , , (, , ), . 2. . , . , , , . . , . (Δ = 4V2), , , 1 /. , , . , . . 3. . . , ( , ) . , , , , , , , . , , . , , . 4. . — , . , . , . . , , , . , St. Jude 19 2,2-4,2 / 19-71 … , . , St. Jude . , , , , , .. . . , , . , , , . . , . . . , . , .
St. Jude. — Medtronic-Hall. Starr-Edwards. Hancock. 5. () . , , , . , , , , , , . . , Burstow . , , , . , Rothbart ., , . 6. . , , , , , . — , Medtronic-Hall, , , , . , , . . . , .. . , , . . , , . ( ). , , . ( ) , , . , — , , , , . , , , , .. , , . . , . , , , , , , , . , , .
— . — . 7. . . , 19 () 30 40 .. , , , , . . 75- , Carbomedics 19 . , , 85 53 .., . , , 31 .. , , . , . . , . ) . , , , . — , , , , . , , , , , . . , , . 1. . , , . , , , . 2. . , , . , , . . , . (.. ) PlSA-, , . 1/2P . 3. . ( ) . , . , , , . , ; . . , , , , . , , — . , . , , , , . , , , .
— St. Jude. — Medtronic-Hall. , , . St. Jude , — , , . ) . , , (1/2P). . , . SMK = 220/1/2P, . , 1/2P 100 , , , , . 1/2P, . . , . , , . 1/2P . 1/2P . , , , , 1/2P . ) : 1. . , . . , , , , , . , — , , , . (3-6 ), . , 0-38% [ ] 0-6% [ ]. .
2. . , — , , , , . 100% . , . — 0-44% . 3. . , . , , , . . , . Medtronic-Hall, , , . , . , , . , . 4. . , . , ( ), . , , , ; . 5. . , , . , , , . , . , , -, , — , , — .
— , ( ), ( ). — . — . , , . . , . . , , ( — , — , s — , i — ). . (1 — , 2 — , 3 — , 4 — ). 6. . , . : — . — , , . , , . — . . , . , . — . , . , . , ( ), , , , . — . , . , . , , T1/2P . , .
— ( )— » « : . : 6.1.2020 |
Источник
Эхокардиография сердца норма у взрослых в таблице
Таблица № 1. Нормальные значения размера, объема и ФВ ЛЖ в двумерной эхокардиографии (Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
BSA: площадь поверхности тела; ФВ: фракция выброса; ЛЖ: левый желудочек; КДР ЛЖ: конечный диастолический диаметр левого желудочка; КДО ЛЖ: конечный диастолический объем левого желудочка; КСО ЛЖ: конечный систолический объем левого желудочка; М: среднее значение; SD: стандартное отклонение Таблица № 2. Эталонные значения объемов ЛЖ в двухмерной эхокардиографии (Lang R et al. ations for chamber quantification. J Am Soc Echo 2005; 18: 1440-1463)
КДО ЛЖ: конечный диастолический объем левого желудочка; КСО ЛЖ: конечный систолический объем левого желудочка Таблица № 3. Расчет и контрольные значения фракции выброса ЛЖ (ФВ ЛЖ) в двумерной эхокардиографии (Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
Таблица № 4. Референтные значения мышечной массы ЛЖ в двумерной эхокардиографии (в соответствии с международным руководством — Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
Таблица № 5. Референтные значения мышечной массы ЛЖ в двумерной эхокардиографии (в соответствии с международным руководством — Lang R et al. ations for chamber quantification. J Am Soc Echo 2005; 18: 1440-1463)
Таблица № 6. Эталонные значения размера ЛП, площади ЛП и объема ЛП в двумерной эхокардиографии (согласно руководству Lang R et al. ations for chamber quantification. J Am Soc Echo 2005; 18: 1440-1463)
КСД ЛП (см): конечный систолический диаметр левого предсердия; ЛП: левое предсердие Таблица № 7. Эталонные значения индекса объема левого предсердия в двумерной эхокардиографии (в соответствии с международным руководством — Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
Таблица № 8. Нормальные значения для фиброзного кольца АК, синусов Вальсальвы, синутобулярного перехода и проксимального отдела восходящей аорты в двумерной эхокардиографии (в соответствии с международным руководством — Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
Таблица № 9. Эталонные значения размеров правого желудочка в двумерной эхокардиографии (в соответствии с международным руководством — Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
ППТ: площадь поверхности тела; ПЖ: правый желудочек; ВТПЖ выносящий тракт правого желудочка; SD: стандартное отклонение Таблица № 10. Значения нормы и отклонения для правого желудочка, его выносящего тракта и легочной артерии в В-режиме на эхокардиографии (согласно руководству Lang R et al. ations for chamber quantification. J Am Soc Echo 2005; 18: 1440-1463)
АК: аортальный клапан; ЛК: клапан легочной артерии; ПЖ: правый желудочек; ВТПЖ: выносящий тракт правого желудочка Таблица № 11. Значения нормы и отклонения для площади правого желудочка в В-режиме на эхокардиографии (согласно руководству Lang R et al. ations for chamber quantification. J Am Soc Echo 2005; 18: 1440-1463)
Таблица № 12. Нормальные значение размера и объема правого предсердия в двумерной эхокардиографии (в соответствии с международным руководством — Lang R et al. ations for chamber quantification by echocardiography in adults. J Am Soc Echo 2015; 28: 1-39)
Таблица № 13. Значения нормы и отклонения размеров правого предсердия в В-режиме на эхокардиографии (согласно руководству Lang R et al. ations for chamber quantification. J Am Soc Echo 2005; 18: 1440-1463)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Источник
Градиент давления — Pressure gradient
В науке об атмосфере градиент давления (обычно воздуха, но в более общем плане любой жидкости ) — это физическая величина, которая описывает, в каком направлении и с какой скоростью давление увеличивается наиболее быстро в определенном месте. Градиент давления — это размерная величина, выраженная в паскалях на метр (Па / м). Математически это получается путем применения оператора del к функции давления от положения. Отрицательный градиент давления известен как плотность силы .
В нефтяной геологии и нефтехимии, относящихся к нефтяным скважинам , и более конкретно в гидростатике , градиенты давления относятся к градиенту вертикального давления в столбе жидкости внутри ствола скважины и обычно выражаются в фунтах на квадратный дюйм на фут (psi / ft ). Этот столб жидкости подвержен сложному градиенту давления вышележащих жидкостей. Путь и геометрия колонны не имеют значения; только вертикальная глубина столбца имеет какое-либо отношение к вертикальному давлению в любой точке в его столбце и градиенту давления для любой заданной истинной вертикальной глубины .
Физическая интерпретация
Понятие градиента давления — это локальная характеристика воздуха (в более общем смысле исследуемой жидкости). Градиент давления определяется только в тех пространственных масштабах, в которых определяется само давление (в более общем смысле гидродинамика ).
В планетных атмосферах (включая Землю ) градиент давления представляет собой вектор, направленный примерно вниз, потому что давление наиболее быстро изменяется по вертикали, увеличиваясь вниз (см. Изменение давления по вертикали ). Значение силы (или нормы ) градиента давления в тропосфере обычно составляет порядка 9 Па / м (или 90 гПа / км).
Градиент давления часто имеет небольшую, но критическую горизонтальную составляющую, которая в значительной степени отвечает за циркуляцию ветра в атмосфере. Горизонтальный градиент давления представляет собой двумерный вектор в результате проекции градиента давления на локальную горизонтальную плоскость. Вблизи поверхности Земли эта сила горизонтального градиента давления направлена от более высокого давления к более низкому. Его конкретная ориентация в любое время и в любом месте сильно зависит от погодных условий. В средних широтах типичный горизонтальный градиент давления может принимать значения порядка 10 -2 Па / м (или 10 Па / км), хотя в пределах метеорологических фронтов встречаются гораздо более высокие значения .
Актуальность погоды и климата
Интерпретация различий в атмосферном давлении между различными местами является фундаментальным компонентом многих метеорологических и климатологических дисциплин, включая прогнозирование погоды . Как указано выше, градиент давления представляет собой одну из основных сил, действующих на воздух, заставляя его двигаться как ветер. Обратите внимание, что сила градиента давления направлена от зон высокого давления к зонам низкого давления. Таким образом, он ориентирован в противоположном направлении от самого градиента давления.
В акустике
В акустике градиент давления пропорционален ускорению звуковой частицы согласно уравнению Эйлера . Звуковые волны и ударные волны могут вызывать очень большие градиенты давления, но это колебательные и часто преходящие возмущения.
Смотрите также
- Неблагоприятный градиент давления
- Плотность силы
- Изобар
- Геопотенциальная высота
- Геострофический ветер
- Примитивные уравнения
- Температурный градиент
Рекомендации
- Коннер А. Перрин (1967) Природа и теория общей циркуляции атмосферы , Всемирная метеорологическая организация, публикация № 218, Женева, Швейцария.
- Роберт Г. Флигл и Джуст А. Басинджер (1980) Введение в физику атмосферы , второе издание, Academic Press, International Geophysics Series, Volume 25 , ISBN 0-12-260355-9 .
- Джон С. Уоллес и Питер В. Хоббс (2006) Наука об атмосфере: вводный обзор , второе издание, Academic Press, Международная серия по геофизике, ISBN 0-12-732951-X .
Внешние ссылки
- Третий оценочный доклад МГЭИК
Источник

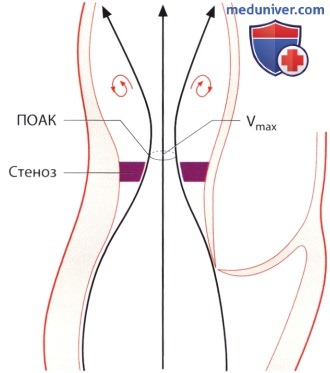 . — .
. — . 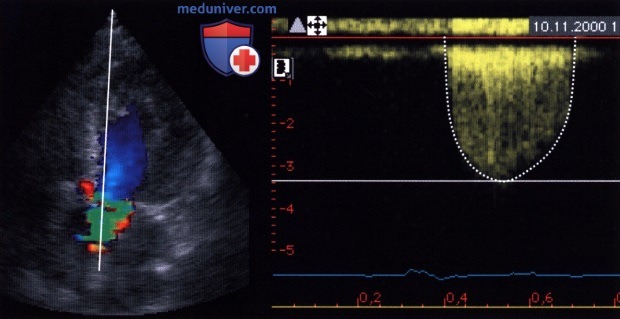 , ( ) ( DPmax 46 ..).
, ( ) ( DPmax 46 ..). 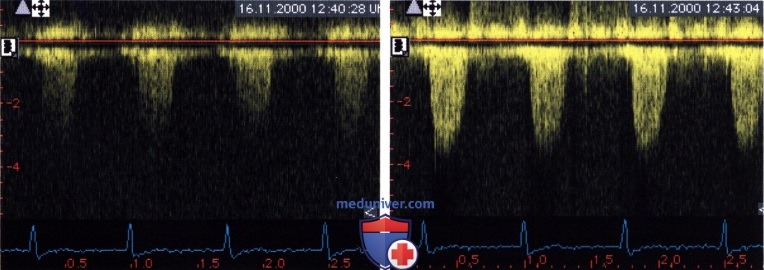 () () , .
() () , .
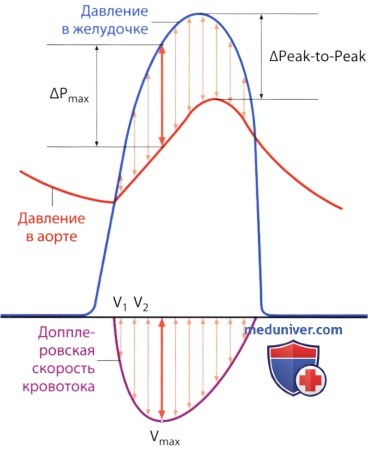 (Peak-to-Peak), , (ΔPmax), Vmax ( ).
(Peak-to-Peak), , (ΔPmax), Vmax ( ). 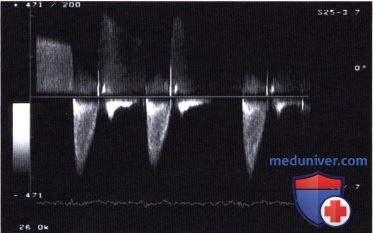 .
. :
: .
.  , (AVA = 1,8 2; ) (AVA = 0,5 2; ). . , , .
, (AVA = 1,8 2; ) (AVA = 0,5 2; ). . , , .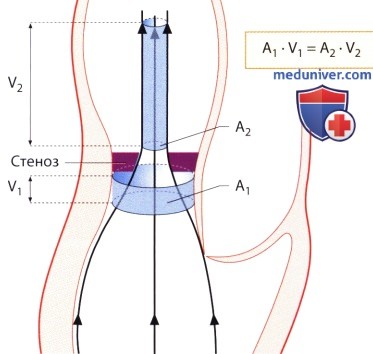 (A2) . (A1), (V1), , A2 : A2 = A1 * (V1/V2).
(A2) . (A1), (V1), , A2 : A2 = A1 * (V1/V2). 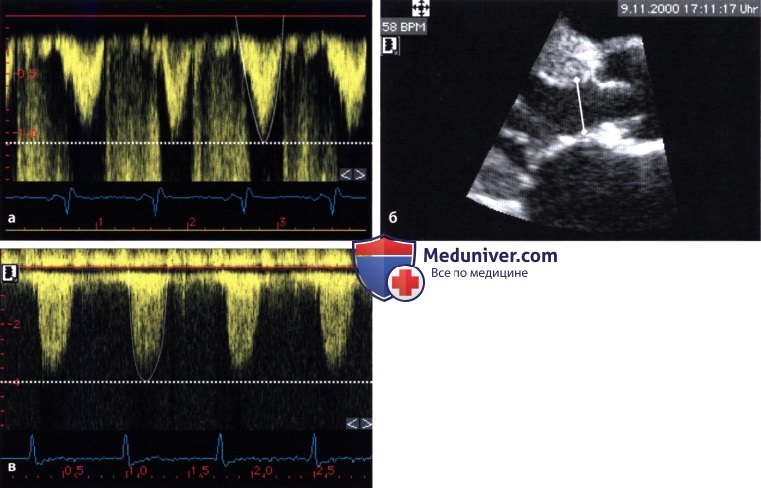 . A2 = A1 * (V1/V2) = (1,22*π*110)/400 = 1,24 2.
. A2 = A1 * (V1/V2) = (1,22*π*110)/400 = 1,24 2.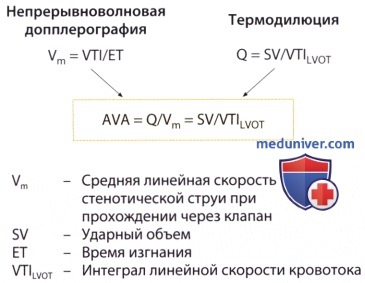 : .
: .
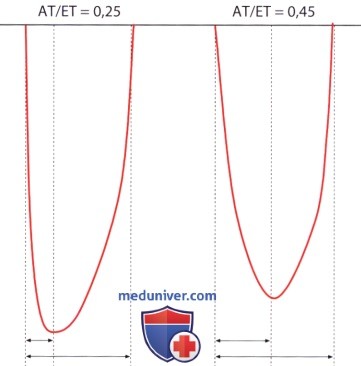 . — , , — . — , — .
. — , , — . — , — .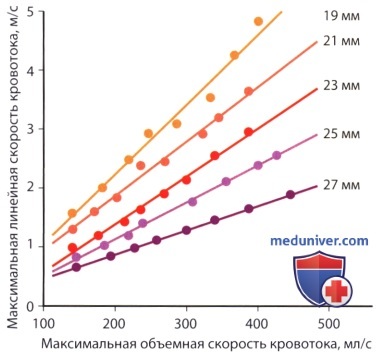 , St. Jude .
, St. Jude .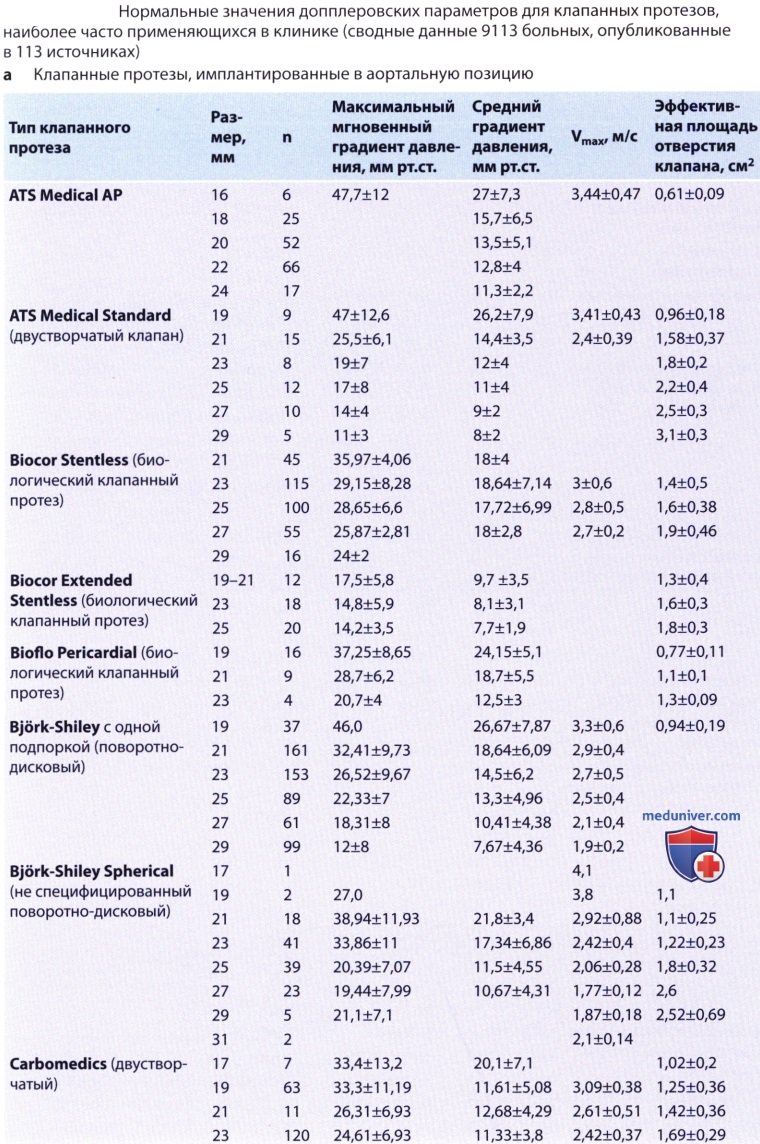
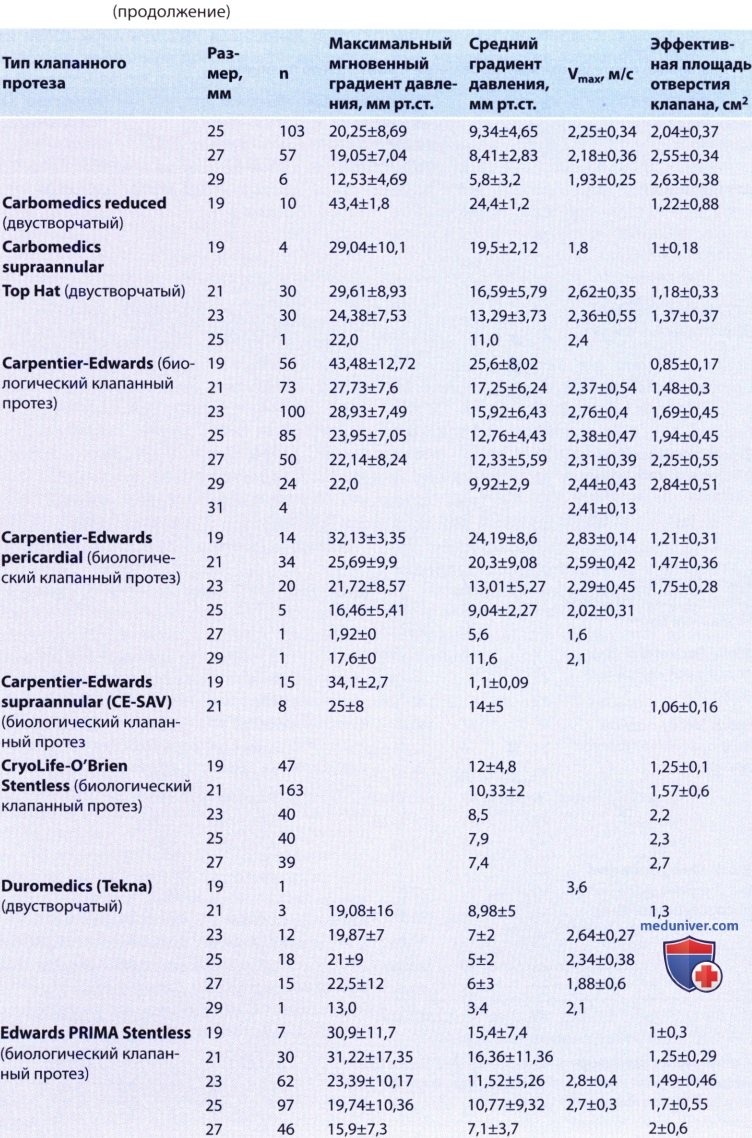
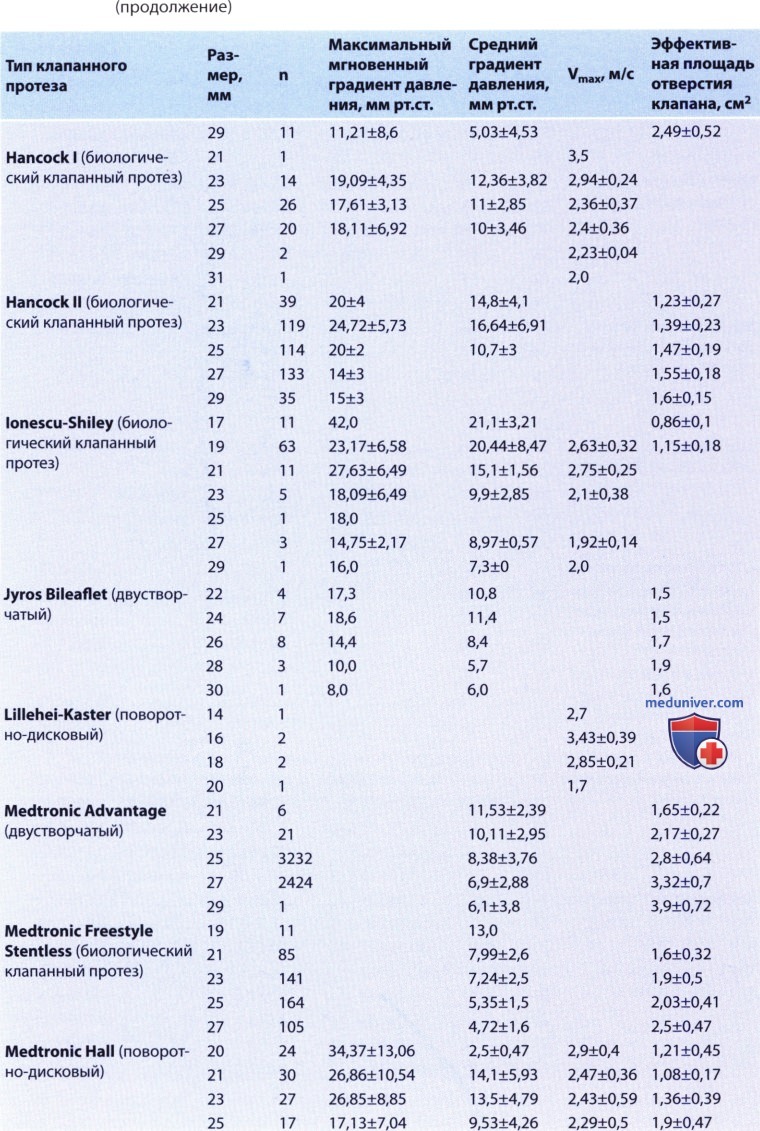
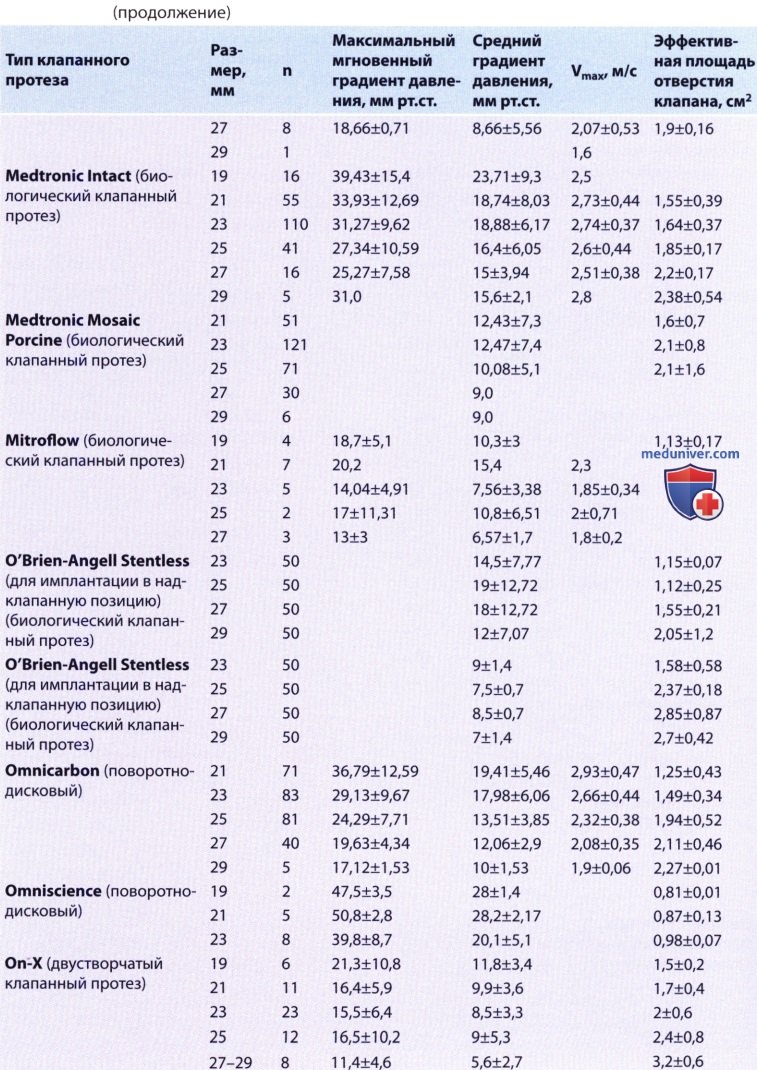
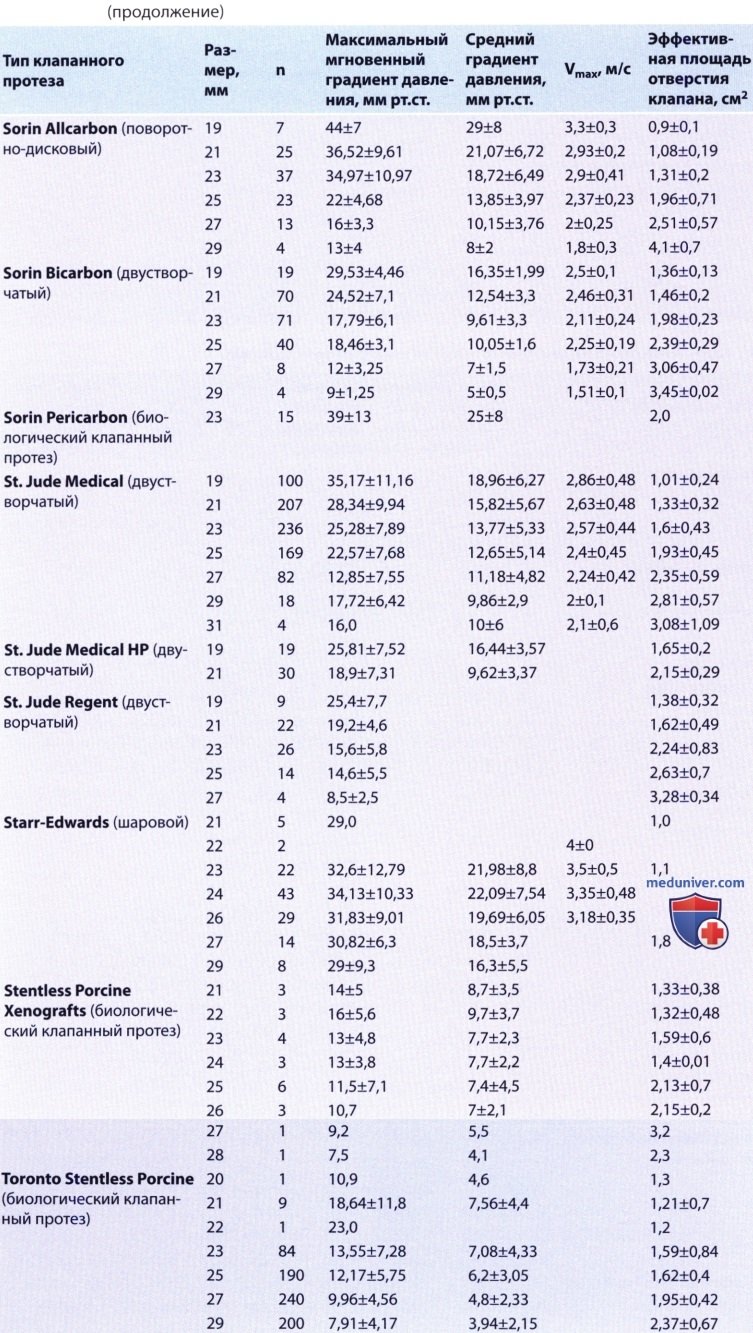
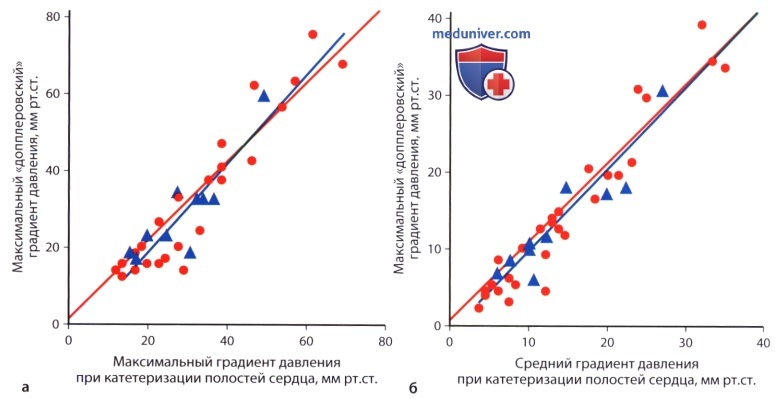 , , , . , — . .
, , , . , — . . 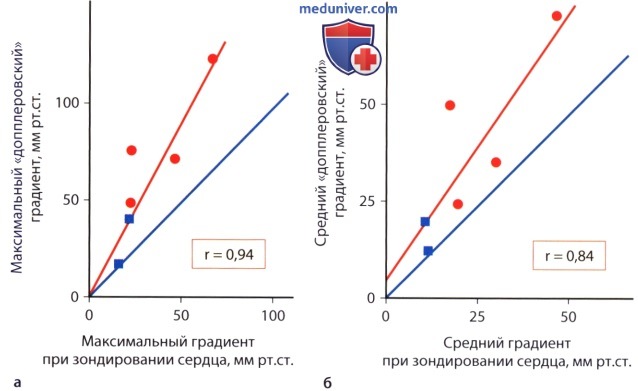 , Starr-Edwards. , , .
, Starr-Edwards. , , . 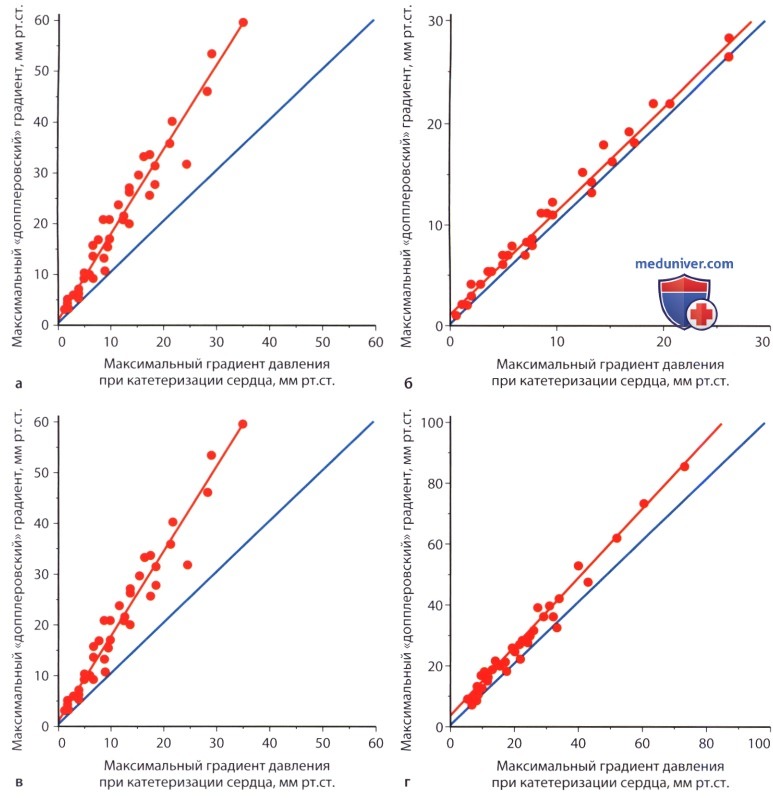 . :
. : .
.  St. Jude , — ( ) 4 ( ).
St. Jude , — ( ) 4 ( ). 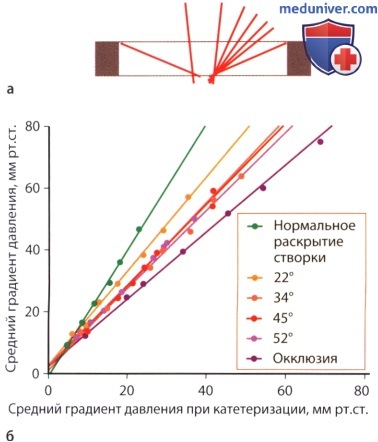 St. Jude ( ):
St. Jude ( ):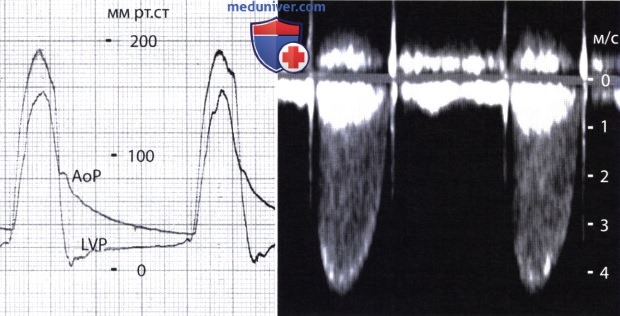 , (LVP) (), , , . , , 31 .. , 53 ..
, (LVP) (), , , . , , 31 .. , 53 ..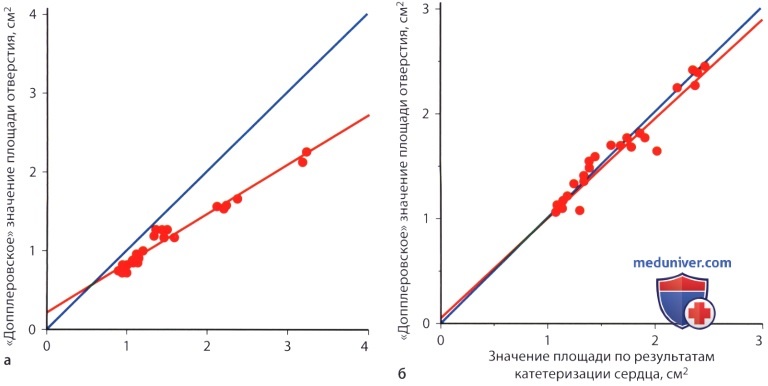 :
: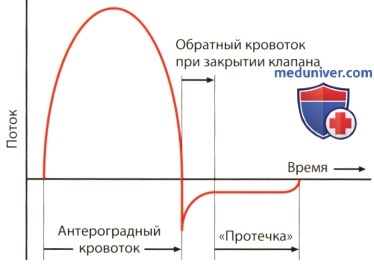 . , . .
. , . .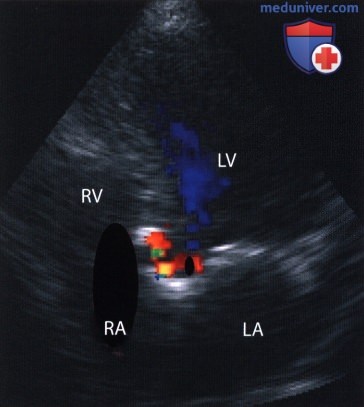 , . .
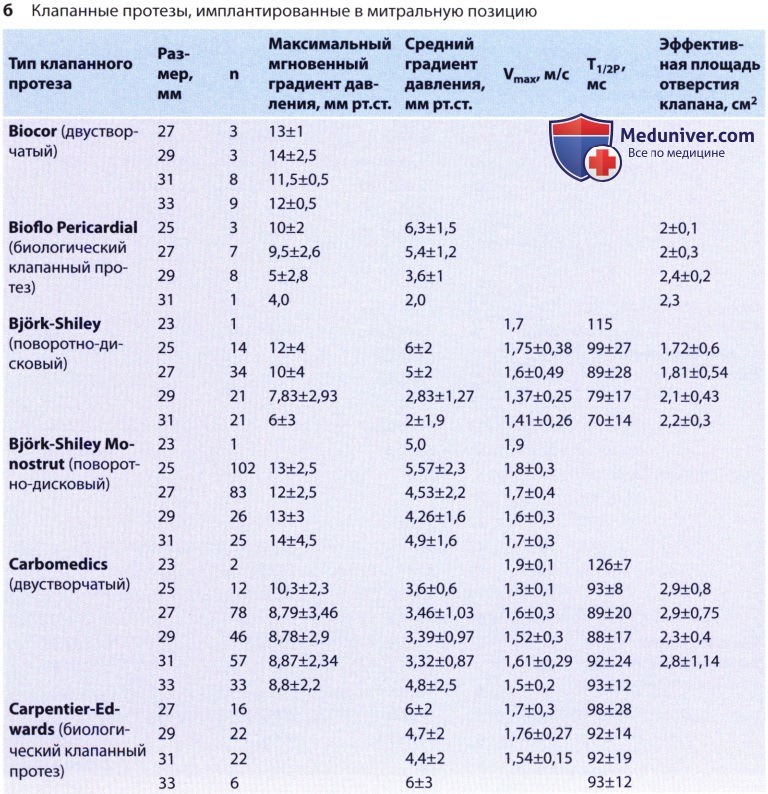
, . . 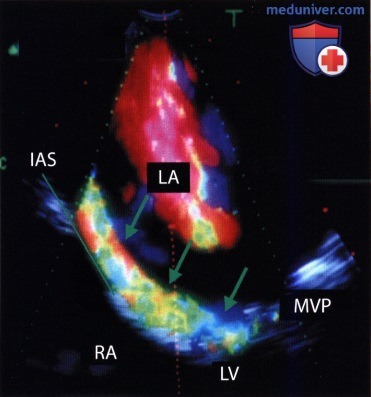 (MVP) . (); ().
(MVP) . (); (). 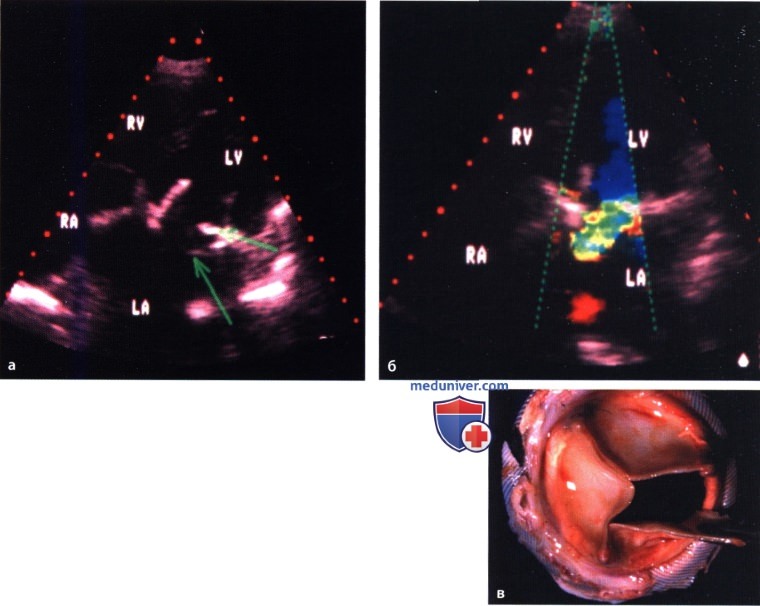 :
: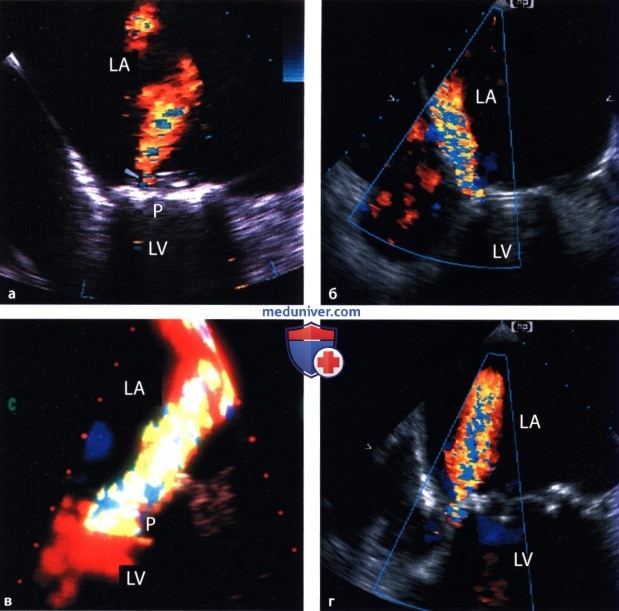 ( — ):
( — ):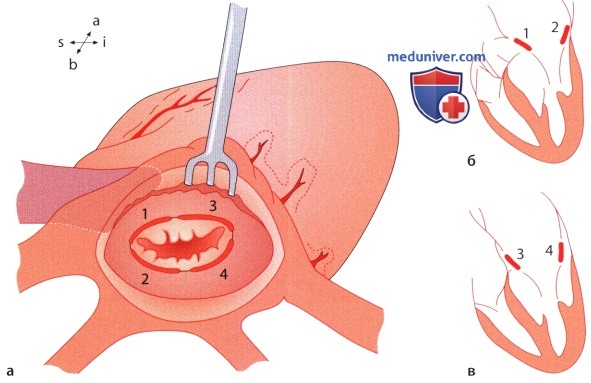 . :
. :