Какое давление внутри мыльного пузыря
Содержание статьи
ыльные пузыри [1987 Асламазов Л.Г., Варламов А.А.
Мыльные пузыри
«Выдуйте мыльный пузырь и смотрите на него: вы можете заниматься всю жизнь его изучением, не переставая извлекать из него уроки физики»,- писал великий английский физик лорд Кельвин. В частности, мыльная пленка является прекрасным объектом для изучения поверхностного натяжения. Сила тяжести здесь практически роли не играет, так как мыльные пленки чрезвычайно тонки и их масса совершенно ничтожна. Поэтому основную роль играют силы поверхностного натяжения, благодаря которым форма пленки всегда оказывается такой, что ее площадь минимально возможная в данных условиях.
Однако почему пленки обязательно мыльные? Почему бы не изучать пленку из дистиллированной воды, ведь ее коэффициент поверхностного натяжения в несколько раз превышает коэффициент поверхностного натяжения мыльного раствора.
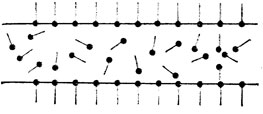
Рис. 1
Дело, оказывается, вовсе не в величине коэффициента поверхностного натяжения, а в структуре мыльной пленки. Мыло богато так называемыми поверхностно-активными веществами, концы длинных молекул которых по-разному относятся к воде: один конец охотно соединяется с молекулой воды, другой к воде безразличен. Поэтому мыльная пленка обладает сложной структурой: образующий ее мыльный раствор как бы «армирован» частоколом упорядочение расположенных молекул поверхностно-активного вещества, входящего в состав мыла* (рис. 1).
* ()
Вернемся к мыльным пузырям. Наверное, каждому доводилось не только наблюдать эти удивительно красивые творения, но и пускать их. Они сферичны по форме и долго могут свободно парить в воздухе. Давление внутри пузыря оказывается больше атмосферного. Избыточное давление обусловлено тем обстоятельством, что мыльная пленка, стремясь еще больше уменьшить свою поверхность, сдавливает воздух внутри пузыря, причем чем меньше его радиус R, тем большим оказывается избыточное давление внутри пузыря. Определим величину этого избыточного давления ΔPсф.
Рис. 2
Поставим мысленный опыт. Пусть поверхностное натяжение пленки пузыря чуть-чуть ослабело, в результате чего его радиус увеличился на величину δR<<R (рис. 2). При этом его внешняя поверхность возрастает на
δS = 4π(R+δR)2 — 4πR2 ≈ 8πRδR
(S = 4πR2 — поверхность сферы), а следовательно, увеличивается и поверхностная энергия пузыря:
δE = σ*(2δS) = 16ππσRδR
(поскольку δЕ уже пропорционально малой величине δR, то изменением коэффициента поверхностного натяжения здесь можно пренебречь).
Заметьте, что в выражении (*) появилась двойка, которой нет в определении поверхностной энергии. Ею мы учли тот факт, что у мыльного пузыря имеется две поверхности — внешняя и внутренняя; при увеличении его радиуса на δR площадь каждой из них возрастает на 8πRδR.
Увеличение поверхностной энергии пузыря произошло за счет работы сжатого в нем воздуха. Считая, что давление в нем при столь малом изменении объема не меняется, можем записать
δAвоз = ΔPсф*δV = δE.(*)
Изменение объема пузыря определяется объемом тонкостенной сферы (рис. 2):
откуда для δЕ находим
Сравнивая это выражение с найденной ранее формулой (*), получаем, что обусловленное поверхностным натяжением избыточное давление внутри сферического мыльного пузыря
Через σ’ = 2σ мы обозначили удвоенный коэффициент поверхностного натяжения жидкости. Понятно, что если бы речь шла об избыточном давлении под одинарной искривленной поверхностью (например, внутри сферической капли жидкости), то оно определялось бы выражением ΔРизб = 2σ/R. Входящая в это выражение величина, обратная радиусу сферы, называется кривизной сферы: ρ = 1/R.

Рис. 3
Итак, мы пришли к важному заключению о том, что избыточное давление пропорционально кривизне сферы. Однако сфера — не единственная форма, которую можно придать мыльному пузырю. Если поместить пузырь между двумя кольцами, то его можно растягивать, пока он не примет форму цилиндра со сферическими «шапками» (рис. 3).
Чему равно избыточное давление внутри такого пузыря? У цилиндрической поверхности кривизна в различных направлениях различна. Вдоль образующей цилиндра кривизна равна нулю (образующая — прямая линия)*, а в сечении, перпендикулярном оси цилиндра, его кривизна равна 1/R, где R — радиус цилиндра. Какое же значение ρ мы должны подставить в предыдущую формулу? Оказывается, разность давлений по разные стороны любой поверхности определяется ее средней кривизной. Что же это за величина?
* ()
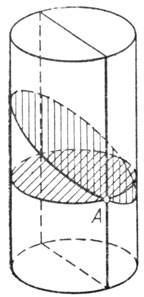
Рис. 4
Проведем через нормаль к поверхности в точке А плоскости. Сечения цилиндрической поверхности этими плоскостями (они называются нормальными сечениями) могут быть окружностью, эллипсом или прямой (рис. 4). Легко видеть, что кривизны этих сечений в точке А различны: максимальной кривизной обладает поперечное сечение — окружность, а минимальной, равной нулю,- прямая (продольное сечение). Средняя кривизна ρср определяется как полусумма максимальной и минимальной кривизны нормальных сечений:
Это определение годится не только для цилиндра; так можно определять среднюю кривизну в данной точке любой поверхности.
У цилиндрической поверхности в любой точке максимальная кривизна ρmax = 1/R, где R — радиус поперечного сечения цилиндра, а ρmin = 0. Поэтому средняя кривизна цилиндра ρц = 1/2R, а избыточное давление внутри цилиндрического пузыря ΔРц = σ’/R.
Как видно, у цилиндрического пузыря избыточное давление такое же, как у сферического пузыря вдвое большего радиуса. Поэтому радиус сферических «шапок» у цилиндрического пузыря будет вдвое больше, чем радиус цилиндра, и они являются сферическими сегментами, а не полусферами.
А что если вообще уничтожить избыточное давление в таком пузыре, заставив, например, лопнуть «шапки»? Казалось бы, так как внутри пузыря нет никакого избыточного давления, поверхность его не должна иметь кривизны. А тем не менее стенки пузыря изгибаются внутрь, и пузырь принимает форму катеноида (от латинского слова «катена» — цепь; эту поверхность можно получить вращением вокруг оси кривой, имеющей формуя подвешенной горизонтально за концы цепи — цепной линии). В чем же Я тут дело?
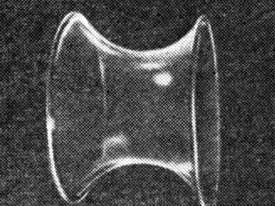
Рис. 5
Присмотритесь к этой поверхности (рис. 5). Обратите внимание на ее узкое место — перехват. Легко видеть, что этот перехват является одновременно и выпуклым, и вогнутым. Его поперечное сечение — окружность, а продольное — цепная линия. Кривизна направления внутрь должна увеличивать давление внутри пузыря, кривизна же направления наружу должна уменьшать его. (Давление под вогнутой поверхностью больше, чем над ней.) В случае катеноида эти кривизны одинаковы по величине, и так как направлены они в противоположные стороны, средняя кривизна равна нулю. Следовательно, внутри такого пузыря нет избыточного давления.
Существует множество других поверхностей, которые кажутся кривыми во всех направлениях, но тем не менее их средняя кривизна равна нулю, и эти поверхности не производят никакого давления. Чтобы получить их, достаточно взять любую гнутую проволочную рамку и погрузить ее в мыльную воду. Вынимая рамку, можно увидеть разнообразные поверхности с нулевой средней кривизной, форма которых зависит от формы рамки. Однако катеноид — единственная, кроме плоскости, поверхность вращения с нулевой средней кривизной.
Одной из задач специальной математической науки — дифференциальной геометрии — является отыскание таких поверхностей с нулевой средней кривизной, натянутых на замкнутые пространственные кривые. Существует точная математическая теорема, утверждающая, что площадь таких поверхностей среди прочих поверхностей, натянутых на ту же кривую, всегда минимальна, и она нам покажется теперь очевидной.
Рис. 6
Мыльные пузыри могут соединяться друг с другом, образуя пену. Несмотря на кажущуюся хаотичность в расположении мыльных пленок в пене, всегда выполняется такой закон: пленки пересекают друг друга лишь под равными углами (см. рис. 6).
Рассмотрим, например, два пузыря, находящихся в контакте друг с другом и имеющих общую перегородку (рис. 7).
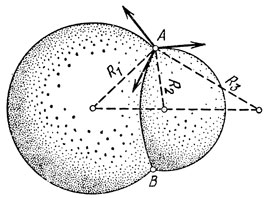
Рис. 7
Избыточные (по сравнению с атмосферным) давления внутри пузырей различны и определяются формулой Лапласа:
Поэтому перегородка должна быть такой, чтобы создавать дополнительное давление внутри пузырей. Следовательно, три пузырей. Следовательно, она должна обладать определенной кривизной. Радиус R3 кривизны перегородки определяется из соотношения
то есть
R3 = R1R3/R2-R1
На рис. 7 изображен разрез пузырей в плоскости, проходящей через их центры. Точки А и В представляют собой точки пересечения с плоскостью чертежа окружности, по которой соприкасаются два пузыря. В любой точке этой окружности встречаются три пленки. Так как их поверхностное натяжение одинаково, то силы их поверхностного натяжения могут «уравновесить» друг друга лишь в том случае, когда углы, под которыми они пересекаются, равны между собой, и следовательно, каждый равен 120°.
Источник
Ответы Mail.ru: Давление внутри мыльного пузыря больше или равно атмосферному? Обоснуйте свой ответ.
Дмитрий Низяев
Искусственный Интеллект
(572356)
7 лет назад
Больше, разумеется. Пленка пузыря образована жидкостью, которая, как известно, имеет поверхностное натяжение. А когда имеешь дело с такими тонкими пленками (сравнимыми с длиной световой волны!) , то поверхностное натяжение становится весьма заметной действующей силой — пленка ведет себе как растянутая резинка, и стремится сжаться, превратиться в каплю шарообразной формы. Но запертый внутри воздух мешает ей сжаться, т. к. то же самое поверхностное натяжение не позволяет пленке хотя бы в одном месте «расступиться», образовать отверстие, в которое воздух мог бы выйти наружу. Поэтому воздух внутри пузыря слегка сжат — всегда. Но с течением времени жидкость постепенно стекает по пленке пузыря в нижнюю его часть. Пузыри в нижней части становится толще, а вверху- истончается. И однажды наступает момент, когда пленка в верхней части становится слишком тонкой и не может удержать давления. В ней образуется разрыв, воздух выходит из пузыря, и вся жидкость получает возможность, наконец, стануться в каплю. Но поскольку стягивание это происходит намного быстрее, чем воздух уходит из пузыря, то пленка стягивается не по радиусам, а как бы скользит вдоль воображаемой сферы огибая оставшийся воздух по дуге. Скорость стягивания очень высокая, и при движении жидкости по дугие возникает сильная центробежная сила. Из-за нее часть воды так и не успевает добраться до нижнего полюса пузыря и слиться в единую каплю — а вмето этого разрывается на отдельные брызги. В Сети можно найти замедленную съемку как лопается мыльный пузырь. Там видно, что после этого события в единую каплю стягивается только часть воды, из нижней половины пузыря — вода, которой было ближе всего добираться до цели. А вот та часть воды, которой пришлось добираться из верхней части пузыря, распадается на мелкие брызги и расшвыривается в стороны. Когда смотришь замедленно, все становится понятно и естественно 🙂
Алексей Юрьев
Гуру
(2759)
7 лет назад
Больше, оболочка дополнительно поджимает. Вспомните воздушный шарик — та же тема. В шарике ведь воздух находиться под повышенным давлением, если открыть впускное отверстие, то воздух из него будет выходить под давлением той же оболочки, если воздух не выходит — он испытывает повышенное давление. Пузырь тот же шарик.
Станислав Лутфуллин
Мастер
(1439)
7 лет назад
давление внутри и снаружи пузыря одинаково. допустим это не так, тогда если бы давление внутри пузыря было больше атмосферного, то его разорвало бы изнутри, если бы давление в нем было меньше, то его «раздавил» бы воздух. вывод давление с обоих сторон равно.
Станислав Суханов
Ученик
(118)
7 лет назад
Аналогия с резиновым шариком верна. Только в одном случае действует сжатие за счет эластичности резинки, а в другом за счет натяжения. Крайне маленькая сила. Тело находится в состоянии покоя, значит приложенные силы равны. Т. Е. Давление на внешние стенки + сила сжатия пузыря равна силе давления на внутренние стенки. Раз сила поверхностного натяжения не равна 0, делаем вывод
Источник
Физика и химия мыльного пузыря. Мнение эксперта
Каждый человек хотя бы один раз в жизни надувал мыльные пузыри. Будь то совсем ранний возраст (малыши, к слову, очень любят это занятие) или ребята постарше (уже более осознанно, да ещё думая, как же сделать их побольше). Мы всегда любуемся множеством переливающихся цветов и правильными формами шариков. Рассказывает Ирина Карпова, педагог дополнительного образования Регионального центра технического творчества.
— Сегодня я хочу рассмотреть мыльные пузыри с точки зрения физики. Мыльный пузырь образуется тонким слоем жидкости с двумя поверхностями, каждая из которых стремится к сокращению, а сам он — к сжатию. Поскольку оболочка мыльного пузыря отличается упругостью, воздух или другой газ внутри него находится под давлением и при первой возможности выходит наружу. Поэтому пузыри лопаются.
Почему мыльный пузырь правильной формы?
Потому что его упругая оболочка стремится сократиться и принять меньшую компактную форму. В природе — это шар. Его поверхность является наименьшей из всех возможных. Однако шар или сфера — не единственная форма, к которой он стремится. Его также можно растягивать при помощи колец.
Откуда берется цвет?
Калейдоскоп цветов, которыми переливаются мыльные пузыри, вызывается сложной структурой света и тем, как он отражается от поверхности. Белый свет состоит из множества цветов, каждый из которых характеризуется собственной длиной волны. Когда свет падает на поверхность мыльного пузыря, часть световых волн сразу же отражается. А часть проходит через стенку пузыря, преломляется в ней и затем отражается от внутренней поверхности. Одни волны встречаются друг с другом, взаимно усиливаясь, оставшиеся — ослабляются. Это явление называется интерференцией волн. В результате на мыльной пленке появляется радуга, поскольку переменная толщина пленки приводит к образованию интерференционных узоров и отражению света в виде лучей различного цвета с собственной длиной волны.
С точки зрения физики мыльные пузыри многогранны. Ничто не заменит их изучение путем опытов и экспериментов. Очень правильно об этом выразился ученый Чарльз Бойс:
«Когда перед нами возникает какой-нибудь новый вопрос, то открываются к его разрешению два пути. Мы можем обратиться к кому-нибудь, кто знаком с этим предметом, или же поискать ответа в книгах, написанных учеными. Это очень хороший путь, если при этом нам посчастливится напасть на сведущего человека или дельную книгу. Но мы можем избрать и другой путь, а именно — путь собственного опыта: мы можем добиться разгадки своими силами. Опыт или эксперимент — это вопрос, который мы ставим природе, и она всегда готова дать нам правильный ответ, если только мы правильно ставим вопрос, т. е. если мы умеем произвести надлежащий опыт. Опыт — это не фокус, не какая-нибудь хитрая штука, которая должна поразить вас. Он показывается не ради красоты и не потому, что может внести разнообразие в монотонность лекций. Если некоторые из моих опытов красивы или могут сделать беседу менее скучной, тем лучше; но главное их значение не в этом: они должны дать вам возможность самим получить правильные ответы на ваши вопросы».
Приходите к нам занятия «Как знать все и ничего?» и «Наука в опытах и экспериментах» и погрузитесь в удивительный мир физики и химии.
Автор: Карпова Ирина Николаевна
Источник
Физика мыльных пузырей
Внимание! Администрация сайта rosuchebnik.ru не несет ответственности за содержание методических разработок, а также за соответствие разработки ФГОС.
- Участник: Красноруцкий Василий Евгеньевич
- Руководитель: Зотова Татьяна Владимировна
Тема: «Физика мыльных пузырей»
Мой учитель по физике предложила поучаствовать в конкурсе «Я учу физику». Я сразу принял это предложение, так как физика стала моим любимым предметом.
Почему я выбрал тему «Физика мыльных пузырей»?
У меня есть маленькая сестрёнка, которая любит всех удивлять. Каждый день я поражаюсь ею. И, конечно, я решил сделать для нее сюрприз!
Мыльный пузырь — тонкая многослойная плёнка мыльной воды, наполненная воздухом, обычно в виде сферы с переливчатой поверхностью. Мыльные пузыри обычно существуют лишь несколько секунд и лопаются при прикосновении или самопроизвольно. Их часто используют в своих играх дети.
Из истории. В 1997 г. – Фэн Янг соорудил самую большую в мире стену из мыльных пузырей высотой около 48 м и площадью 370 м2. Так, в 2007 г. он тоже попал в Книгу рекордов, надув пузырь высотой 1,5 м и шириной 3,3 м, в котором свободно разместились 50 человек.
В мыльном пузыре присутствуют 3 важных элемента:
- Диффузия — это явление, при котором происходит взаимное проникновение молекул одного вещества между молекулами другого. Эта тема в учебнике А.В. Перышкина за 7 класс «Диффузия в газах, жидкостях и твердых телах».
- Закон Паскаля — давление, производимое на жидкость или газ, передаётся в любую точку без изменения во всех направлениях. Эта тема в учебнике А.В. Перышкина за 7 класс «Передача давления жидкостями и газами. Закон Паскаля».
- Закон Архимеда — тела, которые тяжелее жидкости, будучи опущены в неё, погружаются всё глубже, пока не достигают дна, и, пребывая в жидкости, теряют в своём весе столько, сколько весит жидкость, взятая в объёме тел. Эта тема в учебнике А.В. Перышкина за 7 класс «Архимедова сила».
Остановлюсь на каждой теме и попытаюсь ее раскрыть.
Знание явления «диффузии» необходимо было мне для того, чтобы узнать, как сделать наилучший раствор для мыльного пузыря. Как же сделать лучший мыльный раствор? В ходе работы выяснил, что мне необходимы для опытов:
- Вещества, уменьшающие поверхностное натяжение воды, например жидкое мыло или детский шампунь. Чем более чистое мыло (без примесей парфюма или других добавок), тем лучший результат может получиться.
- Вещества, уплотняющие воду. Наиболее часто используется глицерин (который можно купить в аптеке). Также можно использовать сахар, который лучше растворять в тёплой воде. Однако плотность воды может стать слишком большой, поэтому важно соблюдать умеренность.
- Дистиллированная вода. Вода из-под крана содержит ионы кальция, которые связывают мыло. При использовании дистиллированной воды влияние данного эффекта на качество мыльного пузыря значительно ниже.
Это основные компоненты для создания мыльного раствора. В видеоролике будет предложено 3 раствора для мыльного пузыря.
Далее я узнал для чего мне надо знать закон Паскаля. Сейчас я смело могу сказать своей младшей сестре, что мыльный пузырь имеет форму шара, так как давление внутри жидкости или газа во всех направлениях одинаково.
И действительно, почему пузырь имеет форму шара?
Пользуясь источниками интернета, я нашёл ответ на этот вопрос — в мыльном пузыре присутствует тёплый воздух и поэтому мыльный пузырь летает, ведь тёплый воздух легче воздуха. По закону Паскаля можно утверждать, что воздух, внутри мыльного пузыря, будет передаваться во всех направлениях и поэтому пузырь имеет форму шара.
Как же выдуваются мыльные пузыри? Почему некоторые пузыри поднимаются, а потом опускаются?
Для того чтобы выдуть мыльный пузырь необходим хороший мыльный раствор. Мы надуваем мыльный пузырь тёплым воздухом изо рта. Этим воздухом мы создаём силу выталкивания, по которой воздух выталкивает плёнку в трубочке и получается пузырь формы шара. Он поднимается, ведь, как я уже говорил, тёплый воздух легче холодного. Остывая, он опускается, ведь остывший воздух тяжелее тёплого. Здесь всё стало ясно!
Из истории: Житель Швейцарии Ханс Рудольф Сутер выдул мыльный пузырь в длину более чем на 4 метра. Впоследствии его имя было внесено в «Книгу рекордов Гиннеса».
Я задался вопросом: Почему мыльные пузыри на солнце переливаются?
Оказалось, что это можно объяснить тоже при помощи физики. Но пока это явление смог узнать информацию от учителя, так как данная тема будет рассматриваться в 8 классе.
Оказалось, что калейдоскоп цветов, которыми переливаются мыльные пузыри, вызывается сложной структурой света и тем, как он отражается от поверхности пузырей. Белый свет состоит из множества цветов, каждый из которых характеризуется собственной длиной волны. Вот так и переливаются мыльные пузыри.
Я надеюсь, что мой проект вам понравится.
При выполнении практических опытов, я помнил о правилах техники безопасности. Я учитывал, что работать с мыльным раствором надо аккуратно, чтобы он не попадал в глаза. Также, размешивая раствор в стеклянной посуде, я работал с ней осторожно.
Вот ссылка на мой видеоролик: https://drive.google.com/file/d/0Bz70DG5FOyZ9NWZhSW1SZDUwYTA/view?usp=sharing
Источник