Какое давление называется парциальным закон дальтона

Закон Дальтона

В природе и в технике мы очень часто имеем дело не только с одним чистым газом, но со смесью нескольких газов. Например воздух, это смесь азота, кислорода, аргона, углекислого газа и других газов. От чего зависит давление смеси газов?

В 1801 г. Джон Дальтон установил, что давление смеси нескольких газов равно сумме парциальных давлений всех газов, составляющих смесь.

Этот закон получил название закона парциальных давлений газов

Закон ДальтонаПарциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.

Закон Дальтона устанавливает, что давление смеси (идеальных) газов составляет сумму парциальных давлений компонент смеси (парциальное давление компоненты — это давление, которое компонента оказала бы, если бы она одна занимала все пространство, занятое смесью). Этот закон указывает, что на каждую компоненту не воздействует присутствие других компонент и свойства компоненты в смеси не меняются.

Два закона Дальтона

Закон 1 Давление смеси газов равно сумме их парциальных давлений. Из этого следует, что парциальное давление компонента газовой смеси равно произведению давления смеси на молярную долю этого компонента.

Закон 2 Растворимость компонента газовой смеси в данной жидкости при постоянной температуре пропорциональна парциальному давлению этого компонента и не зависит от давления смеси и природы других компонентов.

Законы сформулированы Дж. Дальтоном соотв. в 1801 и 1803.

Уравнение закона Дальтона

Как уже отмечалось, отдельные компоненты смеси газов считаются независимыми. Поэтому каждая компонента создает давление:

[ p = p_i k T quad left(1right), ]

а полное давление равно сумме давлений компонент:

[ p = p_{01} k T + p_{02} k T + cdots + p_{i} k T = p_{01} + p_{02} + cdots + p_{i} quad left(2right),]

где ( p_i )- парциальное давление i газовой компоненты. Это уравнение — закон Дальтона.

При больших концентрациях, больших давлениях закон Дальтона не выполняется в точности. Так как проявляется взаимодействие между компонентами смеси. Компоненты перестают быть независимыми. Дальтон объяснил свой закон с помощью атомистической гипотезы.

Пусть имеется i компонент в смеси газов, тогда уравнение Менделеева — Клайперона будет иметь вид:

[ {(p}_1+p_2+dots +p_i)V=(frac{m_1}{{mu }_1}+frac{m_2}{{mu }_2}+dots +frac{m_i}{{mu }_i})RT quad left(3right), ]

где ( m_i )- массы компонент смеси газа, ( {mu }_i )- молярные массы компонент смеси газа.

Если ввести ( leftlangle mu rightrangle ) такую, что:

[ frac{1}{leftlangle mu rightrangle }=frac{1}{m}left[frac{m_1}{{mu }_1}+frac{m_2}{{mu }_2}+dots +frac{m_i}{{mu }_i}right] quad left(4right), ]

то уравнение (3) запишем в виде:

[ pV=frac{m}{leftlangle mu rightrangle }RT quad left(5right). ]

Закон Дальтона можно записать в виде:

[ p=sumlimits^N_{i=1}{p_i}=frac{RT}{V}sumlimits^N_{i=1}{{nu }_i} quad left(6right). ]

Следствием закона Дальтона можно считать следующее выражение:

[ p_i=x_ip quad left(7right), ]

где ( x_i-молярная концентрация i-го ) газа в смеси, при этом:

[ x_i=frac{{nu }_i}{sumlimits^N_{i=1}{н_i}} quad left(8right), ]

где ( {nu }_i )- количество молей ( i-го ) газа в смеси.

Больше интересного в телеграм @calcsbox

Контейнер объемом 10 литров содержит 1 моль азота и 3 моль водорода при температуре 298 K. Рассчитайте суммарное давление (в атм), если каждый компонент является идеальным газом.

1 моль N2, 1 моль H2, V = 10 л, P = ?

( p = p_{A} + p_{B} = (n_A + n_B)frac{RT}{V} )

( p = (1 + 3)frac{8.2cdot 10^{-2}cdot 298}{10} = 9.78 text{атм} )

Уровень8 класс ПредметФизика СложностьПростая

Определить плотность смеси идеальных газов, если один из компонентов смеси газ массой ( m_1 )и молярной массой ( {mu }_{1,} ) второй газ массой ( m_2 )и молярной массой ( {mu }_2 ). Температура смеси T, давление p.

За основу решения задачи примем закон Дальтона (Давление смеси газов есть сумма парциальных давлений компонент):

[ p=p_1+p_2left(2.1right). ]

парциальные давления компонент найдем из уравнения Менделеева-Клайперона:

[ p_1=frac{RT}{V}frac{m_1}{{mu }_1}, p_2=frac{RT}{V}frac{m_2}{{mu }_2} left(2.2right). ]

Подставим (2.2) в (2.1), получим:

[ p=frac{RT}{V}left(frac{m_1}{{mu }_1}+frac{m_2}{{mu }_2} right)left(2.3right). ]

Плотность по определению:

[ rho =frac{m}{V}=frac{m_1+m_2}{V}=frac{{(m}_1+m_2)p}{RTleft(frac{m_1}{{mu }_1}+frac{m_2}{{mu }_2} right)} ]

Плотность смеси вычисляется по формуле: ( rho =frac{{(m}_1+m_2)p}{RTleft(frac{m_1}{{mu }_1}+frac{m_2}{{mu }_2} right)} ).

Уровень8 класс ПредметФизика СложностьПростая

Источник

Парциальное давление газов — определение, формулы и законы

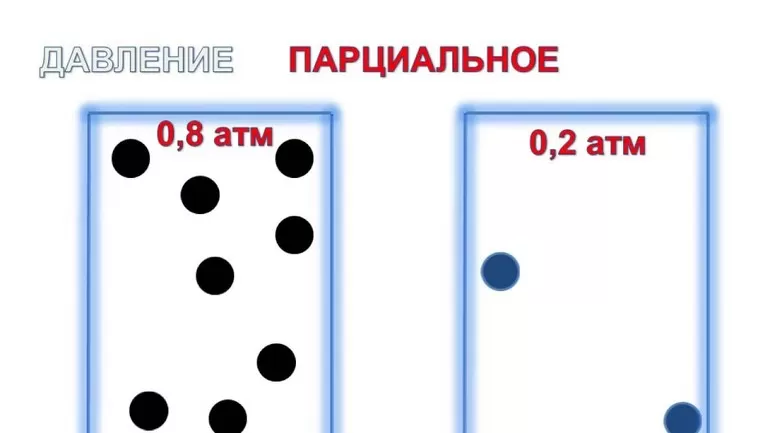
Трактовка закона

Учёный Дальтон в 1801 году сформировал закон парциальных давлений: Па смеси из идеальных газов равняется сумме рi её компонентов. Уравнение имеет следующий вид: Рсм=n (сумма pi), где n — число долей смеси.

Для определения парциального давления в химии используется отдельный компонент из атмосферного воздуха. При расчете учитывается значение каждого отдельного вещества, их число, температуры с объёмами. При необходимости можно найти общий показатель, сложив давление каждого компонента в отдельности.

Каждый газ в сосуде должен обозначаться как «идеальный». При нормальных условиях они взаимодействуют с углекислым газом, водородом, водой, азотом, водяным паром, кислородом, компонентами крови и прочими компонентами из таблицы Менделеева. При этом не образуются соединения. Отдельные молекулы способны сталкиваться между собой, отталкиваясь, но не деформируясь.

Физические и химические задачи решаются с помощью формулы парциального давления (закон открыли учёные Бойль и Мариотт): (k = P x V). Кроме полного варианта, уравнение записывается сокращённо k = PV, где:

• k равно постоянной величине;
• Р — давление;
• V — объем.

Второстепенные значения

Давление может измеряться в разных величинах: процент, паскаль (Па). Смысл последнего: сила в 1 ньютон приложена к площади в 1 кв. м. Если результат такой зависимости записывается в атмосферах, тогда для его нахождения потребуется учесть, что одна атмосфера равняется 101,325 Па.

Температура идеального газа повышается, если увеличивается объём, а снижается, если уменьшается последний показатель. Такое соотношение может называться законом Чарльза, который имеет следующий математический вид: k = V / T. Значение температуры в уравнении измеряется в градусах Кельвина. Оно зависит от градусов Цельсия. Чтобы его найти, прибавляется 273.

Уравнение используется в химии для определения мольной доли (концентрация, которая выражается через отношение количества молей 1 компонента к суммарному числу молей пары веществ, входящих в смесь). Кроме объёма, для газа характерна молярная масса (вес одной доли компонента) и объём. Существуют легкие способы её подсчёта:

1. Стандартная. Измеряется в граммах и килограммах.
2. Молекулярная. Так как газы весят мало, их вес вычисляется в специальной единице измерения — молярная масса. Для её определения суммируется вес составных атомов. Каждый компонент сравнивается с массой карбона, равной 12.

Уравнения Дальтона и Бойля

Физик и химик Дальтон считается первым учёным, предположившим структуру атомных элементов, их свойства. Общее давление вычисляется следующим образом: Р= P1 + P2 + P3. Пример: в колбе содержится по 10 г оксигена и нитрогена. Их общее Р будет равно 20 (10+10). Для вычисления pi используется температура, равная 37 градусам Цельсия.

Чтобы перевести её в градусы Кельвина, значение по Цельсию, равное 37, добавляется к 273. Результат — 310. Для вычисления количества молей газов используется масса, поделённая на молярную. Если уравнение касается нитрогена, вес каждого компонента соответствует цифре 14.

Так как вещество содержит в себе 2 атома, то 14х2, что равно 28. Масса в граммах делится на полученный результат. Таким способом вычисляется количество молей, приблизительно равное 0,4 моль. Чтобы найти аналогичное значение у оксигена, применяется масса 16. Вещество относится к двухатомным газам, поэтому 16х2 равняется 32. По результатам получается, что 0,3 моль оксигена содержится в составе газовой смеси.

Если в задаче указывается общее давление и pi в атмосферах, тогда используется в качестве константы R (0.0821 л атм/K моль). При подстановке данных в уравнение можно узнать Pобщее. Чтобы вычислить ПД нитрогена, 0,4 моль умножается на константу и температуру. Результат делится на 2 литра, что приблизительно равно 5.09 атм. Аналогичные шаги выполняются для вычисления ПД оксигена. Конечный результат равен 3.82 атм.

Свойства веществ

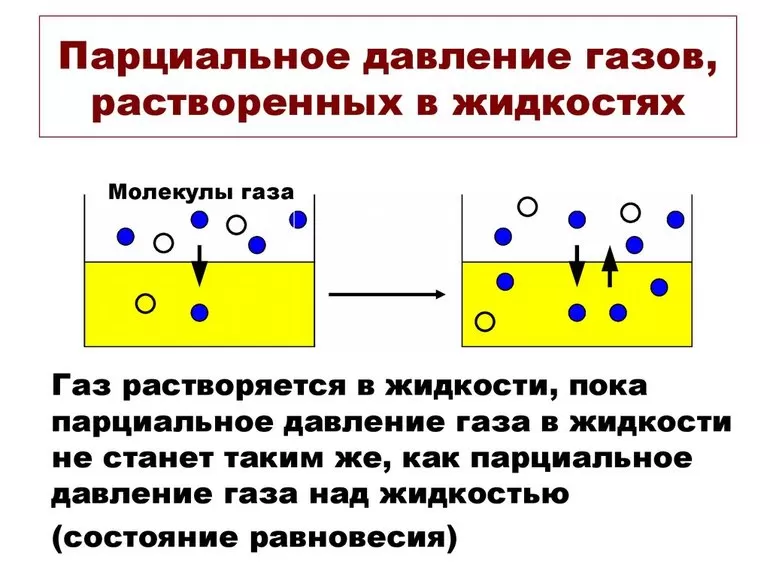
Значение pi газа, растворённого в жидкости, равняется pi того вещества, который образовался бы в фазе газообразования в случае равновесия с жидкостью при аналогичной температуре. Парциальное давление (ПД) измеряется в качестве термодинамической активности молекул вещества.

Газы постоянно вытекают из сферы с высоким ПД в область с низким давлением. Чем больше такая разница, тем быстрее поток. Газам свойственно растворяться, диффундировать, реагировать на ПД. В некоторых случаях показатель не зависит от концентрации газовой смеси.

При решении задач в области химии и физики учитываются свойства газов: сжимаемость и способность расширяться. Они не имеют своей формы, поэтому расширяются до заполнения сосуда, принимая его форму. По аналогичной причине они не имеют объёма. Газ давит на стенки ёмкости по всем направлениям одинаково. Характерное свойство компонентов — способность смешиваться между собой в разных соотношениях.

Так как объём зависит от температуры и давления, поэтому в норме должно быть 0 °C и 760 мм рт. ст. При этом нет места влаги. Если объём считается нормальным, его обозначают стоящей впереди буквой. Подобная зависимость отображается в термодинамике с помощью графика. Если доказана зависимость объема от давления, при этом температура постоянная, используются изотермы (линии, которые изображают на диаграмме процесс с неизменной температурой).

Точки и функции

В законе Бойля чётко указана зависимость объёма от давления при одинаковой температуре. Если данные нанести на график в функцию давления, через точки можно будет провести кривую. Точный эксперимент и незначительный разброс точек позволяют описать объёмное поведение системы с небольшой погрешностью.

Несколько подобных кривых для разных температур во всём диапазоне изученных условий позволяет описать объёмное поведение газа. Одновременно отображаются кривые постоянного давления, которые описывают изменения основных показателей. Чтобы получить окончательные результаты, кривые требуют незначительного сглаживания. Подобные графики сделать самостоятельно менее сложно.

Объём газа при неизменной температуре сильно изменяется с колебаниями давления. Но графически представить такую зависимость в широком диапазоне изменения давлений трудно. Если охвачена широкая область изменения, используются крупные масштабы.

Для упрощения процесса построения на график наносится зависимость произведения Р от давления при одной температуре, что существенно уменьшает область выявления функции. Наибольший эффект получается от применения 1−2 специальных функций объёма, которые называются коэффициентом сжимаемости и остаточным объёмом.

Каждое понятие характеризуется объёмным поведением газа с учётом его отклонений от нормального состояния вещества и созданных идеальных условий. Чтобы упростить поставленную задачу, график отображается на специальной бумаге либо при помощи компьютерных программ. Во втором случае достаточно ввести данные. Сервис самостоятельно строит прямые, кривые и прочие элементы графика.

Простые зависимости лучше отображать в стандартных программах Word. Графические сложные задачи в химии и физике решаются с помощью «Agrafer» — известная компьютерная программа, которая используется не только студентами, но и школьниками.

Источник

Парциальное давление и объем

Когда мы имеем дело со смесями газов, важно знать, что они имеют такие характеристики, как парциальный объем и парциальное давление. Для начала определим, что такое смесь идеальных газов.

Определение 1

Смесь идеальных газов — это смесь нескольких газообразных веществ, которые при заданных условиях не будут вступать в определенные химические реакции.

При смене условий (например, повышении температуры, понижении давления) газовая смесь все же может вступать во взаимодействие. Важный параметр любой такой смеси — так называемая весовая концентрация g i i -ного газа-компонента.

Здесь:

• N — количество газов, из которых состоит смесь;
• x i i -го газа — молярная концентрация указанного газа в составе смеси;
• ν i — количество молей i -го газа, присутствующего в смеси.

Понятие парциального давления

Парциальное давление — это особая характеристика, описывающая состояние компонентов смеси идеальных газов. Сформулируем основное определение:

Определение 2

Парциальным называется давление p i , которое могло бы создаваться i -ым газом в смеси при условии отсутствия остальных газов и сохранения исходного объема и температуры.

Формула парциального давления будет выглядеть так:

p i = m i μ i R T V = μ i R T V

Объем смеси здесь обозначен буквой V , ее температура — T .

Следует подчеркнуть, что поскольку средние кинетические энергии молекул смеси равны, то существует и равенство температур всех компонентов газовой смеси, находящейся в состоянии термодинамического равновесия.

Для нахождения давления смеси идеальных газов нужно воспользоваться законом Дальтона в следующей формулировке:

p = ∑ i = 1 N p i = R T V ∑ i = 1 N ν i

Исходя из него, мы можем выразить парциальное давление так:

p i = x i p .

Понятие парциального объема

У газовой смеси также есть такая характеристика, как парциальный объем.

Определение 3

Парциальный объем V i i -газа в газовой смеси — это такой объем, который мог бы иметь газ при условии отсутствия всех остальных газов и сохранении исходной температуры и объема.

Если речь идет о смеси идеальных газов, то к ней применим закон Амага:

V = ∑ i = 1 N V i

В самом деле, при выражении ν i из формулы выше у нас получится следующее:

ν i = p V i R T ; p = R T V p R T ∑ i = 1 N V i → V = ∑ i = 1 N V i

Для расчета парциального объема газа используется следующая формула:

V i = x i V .

Нам известно, что параметры, определяющие состояние смеси идеальных газов, будут подчиняться уравнению Менделеева-Клайперона. Формула будет выглядеть так:

p V = m μ s m R T .

Все параметры данного уравнения будут относиться ко всей смеси. Это же уравнение удобнее записать так:

p V = m R s m T .

Здесь параметры R s m = R μ s m = R ∑ i = 1 N q i μ i означают удельную газовую постоянную смеси.

Пример 1

Условие: имеется сосуд объемом 1 м 3 , в котором находится 0 , 10 · 10 — 3 к г гелия и 0 , 5 · 10 — 3 к г водорода. Постоянная температура равна 290 К . Вычислите давление смеси и парциальное давление гелия в нем.

Решение

Начнем с вычисления количества молей каждого компонента смеси. Для этого можно использовать формулу:

ν i = m i μ i

Зная, что молярная масса водорода, согласно таблице Менделеева, составляет μ H 2 = 2 · 10 — 3 к г м о л ь , мы можем найти количество его молей в смеси по формуле:

ν H 2 = m H 2 μ H 2

Считаем, что получится:

ν H 2 = 0 , 5 · 10 — 3 2 · 10 — 3 = 0 , 25 ( м о л ь ) .

Точно такие же расчеты проводим и для гелия, зная, что μ H e = 4 · 10 — 3 к г м о л ь :

Теперь с помощью уравнения Менделеева-Клайперона можно найти парциальное давление каждого компонента:

p i V = ν i R T .

Сначала рассчитаем давление водорода:

p H 2 V = ν H 2 R T → p H 2 = ν H 2 R T V

Парциальное давление будет равно:

p H 2 = 0 , 25 · 8 , 31 · 290 1 = 602 , 5 ( П а ) .

Теперь то же самое подсчитываем для гелия:

p H e = 0 , 025 · 8 , 31 · 290 1 = 60 , 25 ( П а ) .

Чтобы найти общее давление смеси газов, сложим сумму давлений ее составляющих:

p = p H 2 + p H e

Подставляем полученные ранее значения и находим нужный результат:

p = 602 , 5 + 60 , 25 = 662 , 75 ( П а ) .

Ответ: общее давление смеси составляет 662 , 75 П а , а парциальное давление гелия в смеси равно 60 , 25 П а .

Пример 2

Условие: дана смесь газов, состоящая из 1 к г углекислого газа и 0 , 5 к г O 2 . Если считать их идеальными, какой объем они будут занимать при давлении в 1 а т м ? Температура смеси равна 300 К .

Решение

Начнем с вычисления общей массы газовой смеси.

m = m O 2 + m C O 2

Значит, m = 1 + 0 , 5 = 1 , 5 .

Переходим к вычислению массовых компонентов смеси:

g O 2 = 0 , 5 1 , 5 = 0 , 33 ; g C O 2 = 1 1 , 5 = 0 , 67 .

Тогда газовая постоянная смеси будет равна:

R s m = R ∑ i = 1 N g i μ i

R s m = 8 , 31 0 , 33 32 · 10 — 3 + 0 , 67 46 · 10 — 3 = 200 Д ж к г К .

Объем смеси вычисляем с помощью уравнения Менделеева-Клайперона:

V s m = m s m R s m T s m p s m

Вспомнив, что по условию давление равно 1 а т м , что равно 10 5 П а , вычислим объем:

V s m = 1 , 5 · 200 · 300 10 5 = 0 , 9 м 3 .

Ответ: при указанных условиях смесь займет объем, равный 0 , 9 м 3 .

Источник