Какое давление идеального газа если масса молекулы
Содержание статьи
Давление идеального газа
Определение давления идеального газа
Определение
Давление идеального газа — это один из самых важных макроскопических параметров, при помощи которого характеризуют состояние системы в молекулярной физике.
Обозначают давление буквой $p$. Если для известной массы идеального газа определены давление и температура (или объем), то полагают, что состояние термодинамической системы в состоянии равновесия определяется однозначно, так как существующие законы и уравнения молекулярно кинетической теории (МКТ) позволяют все остальные параметры вычислить.
В общем случае давление определяют как:
[p={mathop{lim }_{Delta Sto 0} frac{Delta F_n}{Delta S} }left(1right),]
где $F_n$ проекция силы на нормаль к поверхности S данная сила оказывает воздействие, $Delta S$- площадь поверхности.
Идеальный газ оказывает давление на стенки сосуда, в котором он находится, за счет того, что молекулы этого газа движутся и ударяются о стенки сосуда. Давление идеального газа можно найти, применяя основные положение МКТ. При этом получают, что давление идеального газа равно:
[p=frac{1}{3}nm_0{leftlangle v_{kv}rightrangle }^2left(2right),]
где $m_0$ — масса одной молекулы газа; $n$- концентрация молекул газа; $leftlangle v_{kv}rightrangle =sqrt{frac{1}{N}sumlimits^N_{i=1}{v^2_i}}, N $- количество молекул в объеме газа равном $V$. Уравнение (2) называют основным уравнением МКТ. Его можно записать в другом виде, используя среднюю кинетическую энергию молекул ($leftlangle E_krightrangle $):
[p=frac{2}{3}nleftlangle E_krightrangle left(3right).]
С таким важным термодинамическим параметром как термодинамическая температура давление связывает формула:
[p=nkT left(4right),]
где $k$ — постоянная Больцмана. Уравнение (4) называют уравнением состояния идеального газа.
Если проводить изохорный процесс ($V=const$) с некоторой массой идеального газа, то давление его будет подчинено закону Шарля:
[p_2=p_1frac{T_2}{T_1}left(5right),]
где $p_1$- давление газа имеющего температуру $T_1$.
При проведении изотермического процесса ($T=const$) c постоянной массой некоторого газа поведение давления можно характеризовать, используя уравнение:
[p_1V_1=p_2V_2left(6right).]
В соответствии с законом Дальтона давление смеси газов можно найти как сумму давлений каждого газа:
[p=sumlimits^N_{i=1}{p_i} left(7right),]
где $p_i$ — давление каждого газа в отдельности.
Уравнения МКТ, содержащие давление идеального газа
Уравнение Менделеева — Клапейрона (еще один вариант уравнения состояния):
$pV=frac{m}{mu }RT$(8),
где $frac{m}{mu }=nu $ -количество вещества; $m$ — масса газа; $mu $- молярная масса газа; $R$ — универсальная газовая постоянная.textit{}
Определение работы газа в термодинамике:
[A=intlimits^{V_2}_{V_1}{pdV}left(9right).]
Соответственно, первое начало термодинамики для идеального газа в дифференциальном виде запишем как:
[delta Q=pdV+frac{i}{2}nu RdTleft(10right),]
где $i$ — число степеней свободы молекулы газа; $delta Q$ — элементарное количество теплоты, которое получает идеальный газ; $frac{i}{2}nu RdT=dU$ — изменение внутренней энергии термодинамической системы.textit{}
Примеры задач с решением
Пример 1
Задание. В идеальном газе проводят процесс, при котором $p=frac{AU}{V},$ где $U$ — внутренняя энергия газа; $A=const$ для определенного газа. Сравните коэффициенты пропорциональности $A$, если в первом случае газ одноатомный, во втором двух атомный. textit{}
Решение. Внутренняя энергия идеального газа для любого процесса равна:
[U=frac{i}{2}nu RT left(1.1right).]
Состояние идеального газа описывает уравнение Менделеева — Клайперона:
[pV=nu RT left(1.2right).]
Подставим правую часть уравнения, которое описывает заданный в условиях задачи процесс ($p=frac{AU}{V}$) вместо давления в (1.2), имеем:
[frac{AU}{V}V=nu RT left(1.3right).]
Получим из (1.3), что внутренняя энергия вычисляется как:
[U=frac{1}{A}nu RTleft(1.4right).]
Сравним выражения для внутренней энергии (1.1) и (1.4), имеем:
[frac{i}{2}=frac{1}{A}left(1.5right).]
Для одноатомного газа $i=3$; для двухатомного газа (без учета колебаний молекул) $i=5$.
[frac{3}{2}=frac{1}{A_1};; frac{5}{2}=frac{1}{A_2}to frac{A_2}{A_1}=frac{3}{2}cdot frac{2}{5}=frac{3}{5}.]
Ответ. $frac{A_2}{A_1}=frac{3}{5}$
Пример 2
Задание. На рис.1 представлены процессы, проводимые с постоянной массой идеального газа, укажите, как изменяются давления в процессах?
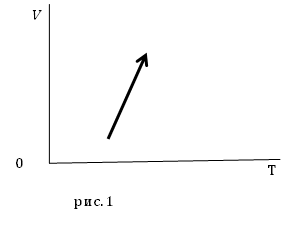
Решение. Уравнение процесса можно аналитически описать уравнением:
[V(T)=AT-B left(2.1right),]
где $A$ и $B$ положительные постоянные величины.
Состояние газа определим при помощи уравнения Менделеева — Клапейрона:
[pV=nu RT left(2.2right).]
Вместо объема подставим уравнение процесса в (2.2):
[pleft(AT-Bright)=nu RTleft(2.3right).]
Раздели обе части (2.3) на температуру:
[frac{pleft(AT-Bright)}{T}=nu Rto pleft(A-frac{B}{T}right)=nu Rto p=frac{nu R}{A-frac{B}{T}} left(2.4right).]
Из уравнения (2.4) следует, что при увеличении температуры $frac{B}{T}$ уменьшается, следовательно, знаменатель дроби правой части выражения (2.4) увеличивается, значит, давление уменьшается.
Ответ. Давление в заданном процессе уменьшается.
Читать дальше: диэлектрический гистерезис.
Источник
Идеальный газ
В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.
Агрегатных состояний точно три?
На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Модель идеального газа
В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.
Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).
Важно знать
Модель идеального газа не может описать ситуацию, когда газ сжимают так сильно, что он конденсируется — переходит в жидкое состояние.
В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.
Свойства идеального газа
- Расстояние между молекулами значительно больше размеров молекул.
- Молекулы газа очень малы и представляют собой упругие шары.
- Силы притяжения между молекулами пренебрежимо малы.
- Молекулы взаимодействуют только при соударениях.
- Молекулы движутся хаотично.
- Молекулы движутся по законам Ньютона.
Среднеквадратичная скорость
Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.
На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.
Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.
Средняя квадратичная скорость
v1, v2, vn — скорости разных молекул [м/с]
N — количество молекул [-]
Давление идеального газа
Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.
Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.
Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.
Эксперимент
Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.
Зависимость давления от других величин
Зависимость давления от объема
В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.
Давление
p = F/S
F — сила [Н]
S — площадь [м2]
То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.
Рассмотрим аналогичный пример с двумя сосудами разной площади.
Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):
Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:
Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.
Зависимость давления от температуры
Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.
В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.
Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.
Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.
С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:
Эта зависимость называется законом Шарля в честь ученого, открывшего ее.
Основное уравнение МКТ
Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.
В основе молекулярно-кинетической теории лежат три положения.
- Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.
Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.
- Атомы и молекулы находятся в непрерывном хаотическом движении.
- Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.
Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.
Основное уравнение МКТ
p = nkT
или
p — давление газа [Па]
n — концентрация [м-3]
T — температура газа [К]
m0 — масса одной молекулы [кг]
v — средняя квадратичная скорость [м/с]
Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.
Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v- и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.
Мы знаем, что кинетическая энергия вычисляется по следующей формуле:
Кинетическая энергия
Ек = mv2/2
Ек — кинетическая энергия [Дж]
m — масса тела [кг]
v — скорость [м/с]
Для молекулы газа формула примет вид:
Средняя кинетическая энергия поступательного движения молекулы
Ек = m0v2/2
Ек — средняя кинетическая энергия поступательного движения молекулы [Дж]
m0 — масса молекулы [кг]
v — скорость молекулы [м/с]
Из этой формулы можно выразить m0v2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Основное уравнение МКТ
p — давление газа [Па]
n — концентрация [м-3]
E — средняя кинетическая энергия поступательного движения молекулы [Дж]
Хранение и транспортировка газов
Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.
Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.
Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.
Источник
СПАДИЛО.РУ
Определение
Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
p=13m0n−v2 | m0- масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
p=13ρ−v2 | ρ — плотность газа |
p=nkT | k — постоянная Больцмана (k = 1,38∙10-3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
Следовательно:
Составим систему уравнений:
Отсюда:
Задание EF19012 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1-2 и 2-3.
Решение
График построен в координатах (V;Ek). Процесс 1-2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1-2 является изобарным, давление во время него не меняется.
Процесс 2-3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2-3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2-3 увеличивается.
Ответ:
• Участок 1-2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2-3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18416 Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой — водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18824 В одном сосуде находится аргон, а в другом — неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF | Просмотров: 2k | Оценить:
Источник