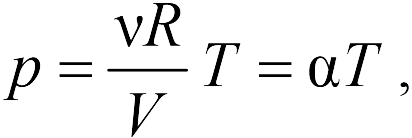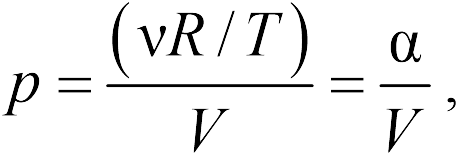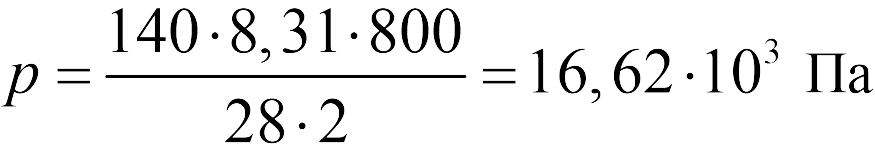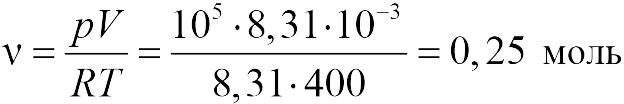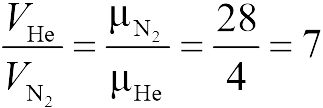Какая зависимость давления на массу
Содержание статьи
Газовые законы
Уравнение состояния идеального газа определяет связь температуры, объема и давления тел.
- Позволяет определить одну извеличин, характеризующих состояние газа, по двум другим (используется в термометрах);
- Определить, как протекают процессы при определенных внешних условиях;
- Определить, как меняется состояние системы, если она совершает работу или получает тепло от внешних тел.
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа)
— универсальная газовая постоянная, R = kNA
Уравнение Клапейрона (объединенный газовый закон)
Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный.
Количественные зависимости между двумя параметрами газа одной и той же массы при неизменном значении третьего параметра называют газовыми законами.
Газовые законы
Закон Бойля — Мариотта
Первый газовый закон был открыт английским ученым Р. Бойлем (1627-1691) в 1660 г. Работа Бойля называлась «Новые эксперименты, касающиеся воздушной пружины». И действительно, газ ведет себя подобно сжатой пружине, в этом можно убедиться, сжимая воздух в обычном велосипедном насосе.
Бойль изучал изменение давления газа в зависимости от объема при постоянной температуре. Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим (от греческих слов isos — равный, therme — тепло).
Независимо от Бойля несколько позднее французский ученый Э. Мариотт (1620-1684) пришел к тем же выводам. Поэтому найденный закон получил название закона Бойля-Мариотта.
Произведение давления газа данной массы на его объем постоянно, если температура не меняется
pV = const
Закон Гей-Люссака
Сообщение об открытии еще одного газового закона было опубликовано лишь в 1802 г., спустя почти 150 лет после открытия закона Бойля-Мариотта. Закон, определяющий зависимость объема газа от температуры при постоянном давлении (и неизменной массе), был установлен французским ученым Гей-Люссаком (1778- 1850).
Относительное изменение объема газа данной массы при постоянном давлении прямо пропорционально изменению температуры
V = V0 αT
Закон Шарля
Зависимость давления газа от температуры при постоянном объеме экспериментально установил французский физик Ж. Шарль (1746-1823) в 1787 г.
Ж. Шарль в 1787 г., т. е. раньше, чем Гей-Люссак, установил и зависимость объема от температуры при постоянном давлении, но он своевременно не опубликовал своих работ.
Давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
p = p0 γT
| Название | Формулировка | Графики |
Закон Бойля-Мариотта- изотермический процесс | Для данной массы газа произведение давления на объем постоянно, если температура не меняется | 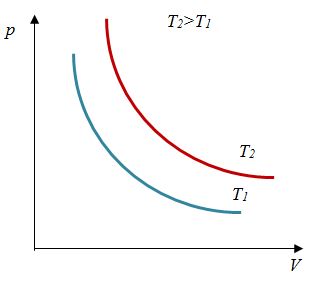   |
Закон Гей-Люссака- изобарный процесс | Для данной массы газа отношение объема к температуре постоянно, если давление не меняется |    |
Закон Шарля- изохорный процесс | Для данной массы газа отношение давления к температуре постоянно, если объем не меняется | 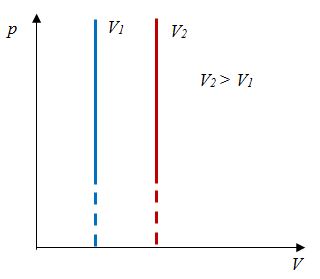 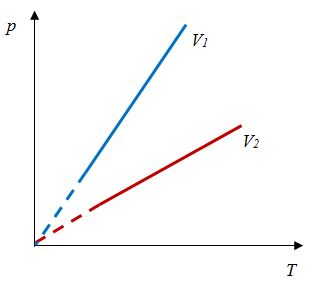 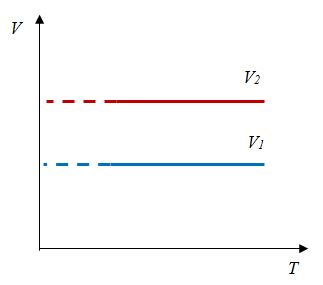 |
Графические задачи
Источник
Формула давления — примеры и условия расчетов

Точные науки
Единица измерения давления в физике и химии — буква «Р» (перевод на латинский — «pressūra). Если наблюдается равновесие внутри и снаружи стенок цилиндра, показатель обозначается «П». По международной системе используются Паскали. Используя формулу давления жидкости и силу, можно прийти к выводу, что 1 Па=1 Н/ 1 кв. м. Так как единица мала, применять её в расчётах сложно.
Из таблицы стандартных конвертеров в физике чаще используются обозначения:
- Бары. 1 Бар=105 Па.
- Торры либо мм ртутного столба (1 торр равен 133 Па).
- Мм вод. столба.
Для определения давления используется сила и площадь: Р = mg / S. Существует зависимость величины от объёма и массы. Для показателя характерно следующее свойство: чем меньше площадь, тем большая сила оказывается на тело. Если давление не изменяется, но увеличивается S, тогда искомый показатель уменьшается.
Главные формулы
При изменении условия агрегатного состояния вещества наблюдаются отличные друг от друга свойства. С учётом этого принципа определяется способ вычисления Р. Для гидростатического состояния используется формула: Р = pgh, где:
- р — плотность;
- g — ускорение;
- h — высота.
Гидростатика применяется к газам. Исключение — вычисление АД. Это объясняется разностью высот и плотностей воздушных масс. От глубины погружения предмета либо объекта зависит значение Р вещества. Так как сила F вычисляется путём умножения m на g, а масса воды — p на V, идеальным вариантом для расчёта давления считается выражение: P = pVg / S. Формула применяется на онлайн-ресурсах, где можно решать задачи по физике и химии.
Если площадь записать в виде S= V/h, тогда Р= pgh. Давление в воде либо иной жидкости вычисляется с учётом изменения верхнего слоя. Это приводит к образованию другого Р. Чтобы найти абсолютную силу, используется формула:
Р = Р0 + 2QH, где:
- Р0 — давление неизменяемого слоя;
- Q — поверхность натяжения жидкого вещества;
- H — среднее значение.
Последний показатель должен сообщаться между первыми двумя, поэтому он считается усреднённым. Для определения значения используются радиусы кривизны: ½ (1/R1+ 1/R2). Каждый вид газа оказывает особенное парциальное давление. Для идеального состояния характерна сумма Р каждого отдельного компонента смеси. Частая ошибка, которую допускают школьники при вычислении давления воздуха — применение только кислорода. Но воздух представлен в виде различных газов:
- аргон;
- азот.
Для нахождения давления воздушных масс используется формула P=P1+P2+P3…
Виды величины

Давление может быть различным (избыточным, барометрическим). Абсолютное понятие характерно для вещества либо объекта, на которое не оказывают влияния иные газы. Показатель измеряется в Паскалях. Он вычисляется по следующему калькулятору: нормальное Р = Р2 + Р3 или Р = Р2 — Р4.
Начало отсчёта идёт от планеты Земля, силы внутри сосуда, из которого удалён воздух. Величина используется во многих термодинамических формулах. Для определения гравитации используется понятие барометрическое либо атмосферное давление. Оно изменяется с учётом температуры атмосферы, времени, высоты.
В норме показатель равняется 760 мм рт. ст., при этом температура должна соответствовать нулю по Цельсию. Чем выше находится объект от Земли, тем ниже оказывается на него давление. Значение уменьшается на 100 Па через каждый восьмой километр.
В горах вода закипает быстрее, чем в домашних условиях: давление воздействует на температуру кипения. Если оно снижается, уменьшается t. Зависимость сохраняется и в обратном порядке. На подобном свойстве функционируют некоторые кухонные приборы: скороварка, автоклав. При повышении номинального Р внутри поднимается температура.
Для расчётов применяется стандартная формула, где используются переменные:
- плотность воздушных масс вблизи уровня Земли;
- высота;
- ускорение;
- температура;
- молярная масса.
Если количество частиц задано в молях, используется формула с постоянной величиной К. При проведении расчётов учитывается вероятность изменения температуры, что связано со сменой погоды, набором высоты, географической широтой. Если из атмосферного Р вычесть измеренное, получится избыточная сила. С учётом результата изменяется название показателя:
- положительный — манометрический;
- отрицательный — вакуумметрический.
Последнее значение не может превышать барометрический уровень. Разница давлений в разных точках называется дифференциальным явлением. Его используют, чтобы определить Р на определённом оборудовании. Такое понятие используется в нефтедобывающей отрасли.
Решение задач

В задачах по физике формулы давления могут выглядеть по-разному. Задача первая: нужно найти Р, оказываемое телом на судно и грунт под водой, когда водолаз находится в движении. Человек весит со снаряжением на суше 180 кг. Площадь стопы равняется 360 кв. см. Сила, с которой человек воздействует на судно равно 180/360 = 0.5 (кгс/см). Используя таблицу, величину можно перевести в Па. Получится 49 кПа. На грунт под водой оказывается сила в 2,46 кПа.
Пример 2: нужно вычислить абсолютное Р воды, если глубина равна 150 м, сила — 765, а масса тела — 1,024 кгс/л. Решение: P = 765/735,6+1,024×150/10=16.4.
Пример 3: ёмкость баллона равна 40 л, давление в нём 150 кгс/см2. Нужно найти V свободных воздушных масс. Решение: начальное Р вычисляется следующим образом: 150+1 = 151 кгс/кв.см. Начальное V равно 40 литров. Свободное V вычисляется p1xнач V/p2=6.04 куб. м. Аналогичным способом решаются задачи, где нужно найти Р любой жидкости, твёрдого объекта, газового вещества.
Измерительные приборы
Можно сэкономить время на расчётах, воспользовавшись специальными приборами, функционирующими путём определения давления в соответствующей среде, что схоже с манометром. Их отличия между собой заключаются в инструкции по эксплуатации, сфере использования, точности, области применения.

Чтобы определить АД, понадобится манометр типа барометра. Для определения разряжения (Па меньше атмосферного) понадобится иная разновидность аппарата — вакуумметр. У человека показатель определяется с помощью сфигмоманометра. Большинство пациентов называют такое оборудование неинвазивным тонометром.
Подобные приборы классифицируются на следующие подвиды:
- ртутные механические;
- полуавтоматические;
- автоматические цифровые.

Их погрешность зависит от материалов, используемых в процессе производства и области измерения. Некоторые устройства одновременно измеряют давление и пульс. Они работают автоматически от батареек. За счёт наличия цифрового табло легко узнать результат. Более точными считаются механические.
Чтобы определить Р, понадобится надеть манжет на правую руку больного. Зажав механизм, производится накачка груши. Максимальный и минимальный пределы начинаются с появления, а затем с исчезновения характерного стука. Постепенно механизм ослабляется. Для получения точных данных потребуется опыт работы с механическим тонометром и внимательность. Если наблюдаются колебания давления в воздухе, понадобится дифнамометр либо манометр.
Источник
Глава 13. Газовые законы
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
(13.1) |
где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
(13.2) |
Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
(13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа
| (13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
| (13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
|
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
| (13.5) |
где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
|
Второй график следует из соотношения
| (13.6) |
где — постоянная при постоянном объеме.
Для изотермического процесса
|
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
| (13.7) |
где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
| (13.8) |
где 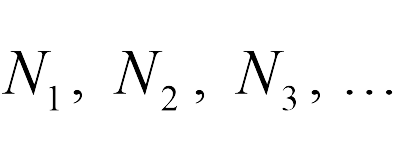 — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
— число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. 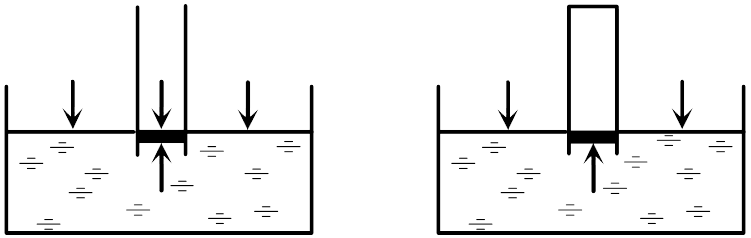 Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).
 Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).
 Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева
|
получим
|
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
|
(ответ 1).
Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия | для азота |
где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
|
(ответ 4).
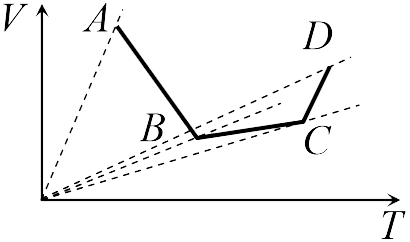
Если бы точки, отвечающие состояниям 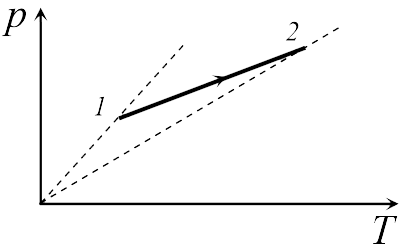 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
|
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем
|
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси — это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
|
(ответ 4). Здесь — масса газа, — масса одной молекулы газа.
Источник