Какая связь между скоростью и давлением
Содержание статьи
Закон Бернулли
Рисунок из «Гидродинамики» Д. Бернулли: из-за течения по трубе, компенсирующего расход через правое отверстие О, давление в трубе меньше, чем в сосуде слева.
Зако́н Берну́лли[1] (также уравне́ние Берну́лли[2][3], теоре́ма Берну́лли[4][5] или интегра́л Берну́лли[2][6][7]) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением. Согласно этому закону, если вдоль линии тока давление жидкости возрастает, то скорость течения убывает, и наоборот. Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости[2] (то есть без вязкости и теплопроводности).
История[править | править код]
Для случая несжимаемой жидкости результат, эквивалентный современному уравнению Бернулли, был опубликован в 1738 году Даниилом Бернулли[K 1]. В современном виде интеграл был опубликован Иоганном Бернулли в 1743 году[11] для случая несжимаемой жидкости, а для некоторых случаев течений сжимаемой жидкости — Эйлером в 1757 году[12].
Интеграл Бернулли в несжимаемой жидкости[править | править код]
Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что величина сохраняет постоянное значение вдоль линии тока:
Здесь
— плотность жидкости; — скорость потока; — высота; — давление; — ускорение свободного падения.
Элементарный вывод уравнения Бернулли из закона сохранения энергии
Элементарный вывод уравнения Бернулли из закона сохранения энергии приведён, например, в учебнике Д. В. Сивухина[13]. Рассматривается стационарное движение жидкости вдоль линии тока, изображённое на рисунке. Слева на объем жидкости, первоначально заключённый между двумя сечениями и , действует сила , а справа — противоположного направления сила . Скорость и давление в сечениях 1 и 2, а также их площади обозначены нижними индексами 1 и 2. За бесконечно малое время левая граница этого объёма жидкости сместилась на малое расстояние , а правая — на расстояние . Работа, совершённая силами давления, равна:
В начале интервала времени объем жидкости, заключённый между двумя поверхностями и , состоит из левого голубого элемента и средней синей части, в конце этого интервала сместившийся объём состоит из средней синей части и правого голубого элемента. Так как течение стационарное, вклад синего фрагмента в энергию и массу обсуждаемого объёма жидкости не меняется, а сохранение массы позволяет заключить, что масса левого голубого элемента равна массе правого голубого элемента: Поэтому работа сил, выражение для которой можно преобразовать к виду: равна изменению энергии, равному, в свою очередь, разности энергий правого голубого элемента и левого голубого элемента .
Для несжимаемой жидкости можно, во-первых, в выражении для работы положить и, во-вторых, в выражении для энергии элемента жидкости ограничиться кинетической и потенциальной энергией: После этого равенство даёт: , или .
Константа в правой части (может различаться для различных линий тока) иногда называется полным давлением[2]. Могут также использоваться термины «весовое давление» , «статическое давление» и «динамическое давление» . По словам Д. В. Сивухина[13], нерациональность этих понятий отмечалась многими физиками.
Размерность всех слагаемых — единица энергии на единицу объёма. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Третье слагаемое по своему происхождению является работой сил давления (см. приведённый выше вывод уравнения Бернулли), но в гидравлике может называться «энергией давления» и частью потенциальной энергии[14]).
Вывод формулы Торричелли из закона Бернулли[править | править код]
Иллюстрация формулы Торричелли
В применении к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда закон Бернулли даёт равенство полных давлений на свободной поверхности жидкости и на выходе из отверстия:
где
— высота столба жидкости в сосуде, отсчитанная от уровня отверстия, — скорость истечения жидкости, — атмосферное давление.
Отсюда: . Это — формула Торричелли. Она показывает, что при истечении жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты . Или, если истекающую из малого отверстия в сосуде струю направить вверх, в верхней точке (в пренебрежении потерями) струя достигнет уровня свободной поверхности в сосуде[15].
Другие проявления и применения закона Бернулли[править | править код]
Закон Бернулли объясняет эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем в широкой части
Приближение несжимаемой жидкости, а с ним и закон Бернулли справедливы и для ламинарных течений газа, если только скорости течения малы по сравнению со скоростью звука[16].
Вдоль горизонтальной трубы координата постоянна и уравнение Бернулли принимает вид . Отсюда следует, что при уменьшении сечения потока из-за возрастания скорости давление падает. Эффект понижения давления при увеличении скорости потока лежит в основе работы расходомера Вентури[17] и струйного насоса[1].
Закон Бернулли объясняет, почему суда, движущиеся параллельным курсом, могут притягиваться друг к другу (например, такой инцидент произошёл с лайнером «Олимпик»)[18].
Применение в гидравлике[править | править код]
Последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Для технических приложений часто уравнение Бернулли записывается в виде, в котором все члены разделены на «удельный вес» :
где имеющие размерность длины члены в этом уравнении могут иметь следующие названия:
— гидравлическая высота[4] или напор[19], — нивелирная высота[4], — пьезометрическая высота[4] или (в сумме с нивелирной высотой) гидростатический напор[19], — скоростная высота[4] или скоростной напор[19].
Закон Бернулли справедлив только для идеальных жидкостей, в которых отсутствуют потери на вязкое трение. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, приближённо учитывающих различные «гидравлические потери напора»[19].
Интеграл Бернулли в баротропных течениях[править | править код]
Уравнение Бернулли может быть выведено и из уравнения движения жидкости[K 2][K 3]. При этом течение предполагается стационарным и баротропным. Последнее означает, что плотность жидкости или газа не обязательно постоянна (как у предполагавшейся ранее несжимаемой жидкости), но является функцией только давления: , что позволяет ввести функцию давления[22] В этих предположениях величина
постоянна вдоль любой линии тока и любой вихревой линии. Соотношение справедливо для течения в любом потенциальном поле, при этом заменяется на потенциал массовой силы .
Вывод интеграла Бернулли для баротропного течения
Для безвихревых баротропных течений, скорость которых может быть выражена в виде градиента потенциала скорости , интеграл Бернулли в виде [K 4] сохраняется также в нестационарных течениях, причём постоянная в правой части имеет одинаковое значение для всего течения[25].
Формула Сен-Венана — Ванцеля[править | править код]
Если в течении совершенного газа выполняется адиабатический закон[26]
то уравнение Бернулли выражается так[27] (вкладом от силы тяжести обычно можно пренебречь):
вдоль линии тока или вихревой линии. Здесь — показатель адиабаты газа, выражающийся через теплоёмкости при постоянном давлении и при постоянном объёме, — давление и плотность газа, — условно выбранные постоянные (одинаковые для всего течения) значения давления и плотности.
С помощью полученной формулы находят скорость газа, вытекающего из сосуда с высоким давлением через малое отверстие. Удобно давление и плотность газа в сосуде, скорость газа в котором равна нулю, принять за тогда скорость истечения выражается через внешнее давление по формуле Сен-Венана — Ванцеля[28]:
Термодинамика закона Бернулли[править | править код]
Из термодинамики следует, что вдоль линии тока любого стационарного течения идеальной жидкости
где — энтальпия единицы массы, — гравитационный потенциал (равный для однородной силы тяжести), — энтропия единицы массы.
Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений
Интеграл Бернулли применяют в инженерных расчётах, в том числе для сред, весьма далёких по своим свойствам от идеального газа, например для водяного пара, используемого в качестве теплоносителя в паровых турбин. При этом могут использоваться так называемые диаграммы Молье, представляющих удельную энтальпию (по оси ординат) как функцию удельной энтропии (по оси абсцисс) и например давления (или температуры) в виде семейства изобар (изотерм). В этом случае последовательность состояний вдоль линии тока лежат на некоторой вертикальной линии (). Длина отрезка этой линии, отсекаемого двумя изобарами, соответствующего начальному и конечному давлению теплоносителя, равен половине изменения квадрата скорости[31].
Обобщения интеграла Бернулли[править | править код]
Интеграл Бернулли также сохраняется при переходе потока через фронт ударной волны, в системе отсчета, в которой ударная волна покоится[32]. Однако при таком переходе энтропия среды не остаётся постоянной (возрастает), поэтому соотношение Бернулли является лишь одним из трёх соотношений Гюгонио, наряду с законами сохранения массы и импульса, связывающих состояние среды за фронтом с состоянием среды перед фронтом и со скоростью ударной волны.
Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений[33]), в магнитной гидродинамике[34], феррогидродинамике[35]. В релятивистской гидродинамике, когда скорости течения становятся сравнимыми со скоростью света , интеграл формулируется в терминах релятивистски инвариантных[36] удельной энтальпии и удельной энтропии[37].
Комментарии[править | править код]
- ↑ В записи Д.Бернулли в явном виде не фигурировало внутреннее давление в жидкости[8][9][10].
- ↑ «…[Вывод теоремы Бернулли из уравнения энергии] обедняет содержание теоремы Бернулли … Интеграл Бернулли, вообще говоря, не зависит от уравнения энергии, хотя действительно совпадает с ним для изоэнтропического и адиабатического движения совершенного газа»[20].
- ↑ «Два … пути получения уравнения Бернулли не эквивалентны. При энергетическом выводе нет необходимости в предположении об изэнтропичности течения. При интегрировании уравнения движения интегралы Бернулли получаются не только вдоль линий тока, но и вдоль вихревых линий»[21].
- ↑ В русскоязычной литературе интеграл Бернулли для потенциальных течений несжимаемой или баротропной жидкости известен как интеграл Коши — Лагранжа[25]
Примечания[править | править код]
- ↑ 1 2 Ландсберг Г. С. Закон Бернулли, 1985.
- ↑ 1 2 3 4 Вишневецкий С. Л. Бернулли уравнение, 1988.
- ↑ Титьенс О., Прандтль Л. Гидро- и аэромеханика, 1933.
- ↑ 1 2 3 4 5 Лойцянский Л. Г. Механика жидкости и газа, 2003, §24. Теорема Бернулли.
- ↑ Милн-Томсон Л. М. Теоретическая гидродинамика, 1964.
- ↑ Седов Л. И. Механика сплошной среды, 1970.
- ↑ Чёрный Г. Г. Газовая динамика, 1988.
- ↑ Трусделл К. Очерки по истории механики, 2002.
- ↑ Михайлов Г. К., 1999, с. 17.
- ↑ Darrigol O. A history of hydrodynamics, 2005, с. 9.
- ↑ Трусделл К. Очерки по истории механики, 2002, с. 255, 257.
- ↑ Euler L. Continuation des recherches, 1755 (1757), с. 331.
- ↑ 1 2 Сивухин Д. В. Механика, 1989, §94. Стационарное движение идеальной жидкости. Уравнение Бернулли.
- ↑ Чугаев Р. Р. Гидравлика. — Л.: Энергия, 1975. — 600 с.
- ↑ Сивухин Д. В. Механика, 1989, §95. Примеры на применение уравнения Бернулли. Формула Торричелли.
- ↑ Сивухин Д. В. Механика, 1989, §94, формула (94.6).
- ↑ Молоканов Ю. К. Процессы и аппараты нефтегазопереработки. — М.: Химия, 1980. — С. 60. — 408 с.
- ↑ Я. И. Перельман. Отчего притягиваются корабли?. Дата обращения: 27 декабря 2018.
- ↑ 1 2 3 4 5 Напор, 1992.
- ↑ Бэтчелор Дж. Введение в динамику жидкости, 1973, Примечание Г. Ю. Степанова, с. 208.
- ↑ Гольдштейн Р. В., Городцов В. А. Механика сплошных сред, 2000, с. 104.
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (9).
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (7).
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VIII. §2, уравнение (2.1).
- ↑ 1 2 Лойцянский Л. Г. Механика жидкости и газа, 2003, §42. Интеграл Лагранжа — Коши.
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (29).
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (30).
- ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (31).
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (2.4).
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, §85.
- ↑ Голубкин В. Н., Сизых Г. Б. О некоторых общих свойствах плоскопараллельных течений вязкой жидкости // Известия АН СССР, серия Механика жидкости и газа : журнал. — 1987. — № 3. — С. 176-178. — doi:10.1007/BF01051932.
- ↑ Куликовский А. Г., Любимов Г. А. Магнитная гидродинамика. — М.: Физматлит, 1962. — С. 54. — 248 с.
- ↑ Розенцвейг Р. Феррогидродинамика / Пер. с англ. под ред. В. В. Гогосова. — М.: Мир, 1989. — С. 136. — 359 с. — ISBN 5-03-000997-3.
- ↑ Зубарев Д. Н., Релятивистская термодинамика, 1994.
- ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (134.11).
Литература[править | править код]
- Бэтчелор Дж. Введение в динамику жидкости / Пер. с англ. под ред. Г. Ю. Степанова. — М.: Мир, 1973. — 760 с.
- Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова-Бома эффект — Длинные линии. — С. 187. — 704 с.
- Гольдштейн Р. В., Городцов В. А. Механика сплошных сред. Часть 1. — М.: Физматлит, 2000. — 256 с. — ISBN 5-02-015555-1.
- Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333-334. — 704 с. — ISBN 5-85270-087-8.
- Ландау, Л. Д., Лифшиц, Е. М. Гидродинамика. — Издание 5-е, стереотипное. — М.: Физматлит, 2001. — 736 с. — («Теоретическая физика», том VI). — ISBN 5-9221-0121-8.
- Лойцянский Л. Г. Механика жидкости и газа. — М.: Дрофа, 2003. — 842 с. — ISBN 5-7107-6327-6.
- Милн-Томсон Л. М. Теоретическая гидродинамика. — М.: Мир, 1964. — 656 с.
- Михайлов Г. К. Становление гидравлики и гидродинамики в трудах петербургских академиков (XVIII) // Известия Академии наук, серия Механика жидкости и газа : журнал. — 1999. — Вып. 6. — С. 7-25.
- Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный компрессор — Пойнтинга теорема. — С. 242. — 672 с. — ISBN 5-85270-019-3.
- Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
- Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
- Сивухин Д. В. Общий курс физики. — Издание 3-е, исправленное и дополненное. — М.: Наука, 1989. — Т. I. Механика. — 576 с. — ISBN 5-02-014054-6.
- Титьенс О., Прандтль Л. Гидро- и аэромеханика. — М.-Л.: ГТТИ, 1933. — Т. 1. — 224 с.
- Трусделл К. Очерки по истории механики. — М. — Ижевск: Институт компьютерных исследований, 2002. — 316 с. — ISBN 5-93972-192-3.
- Фабер Т. Е. Гидроаэродинамика / Пер. с англ. под ред. А. А. Павельева. — М.: Постмаркет, 2001. — 560 с. — ISBN 5-901095-04-9.
- Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — 424 с. — ISBN 5-02-013814-2.
- §182. Закон Бернулли // Элементарный учебник физики / Под ред. Г. С. Ландсберга. — М.: Наука, 1985. — Т. 1. Механика. Теплота. Молекулярная физика.
- Darrigol O. Worlds of flow. A history of hydrodynamics from the Bernoullis to Prandtl. — Oxford: Oxford University Press, 2005. — 356 с. — ISBN 978-0-19-856843-8.
- Euler L. Continuation des recherches sur la théorie du mouvement des fluides // Mémoires de l’Académie royale des sciences et belles lettres. — Berlin, 1755 (1757). — Т. 11. — С. 316-361.
- Truesdell, Clifford Ambrose. Rational fluid mechanics, 1687-1765. Editor’s duction to Euleri Opera omnia II 12 // Leonardi Euleri. Opera Omnia. — Lausanne: Auctoritate et Impensis, Societas Scientiarum Naturalium Helveticae, 1954. — Т. 12. — С. I-CXXV. — (II).
Ссылки[править | править код]
- Русский перевод трактата Даниила Бернулли, в котором впервые появляется интеграл (закон) Бернулли
Источник
Связь давления и скорости в потоке
Связь давления и скорости в потоке жидкости — обратная: если в каком-то месте потока скорость увеличивается, то давление здесь малó, и, наоборот, там, где скорости невелики, давление повышенное. Эту закономерность объясним на основе уравнения Бернýлли.
Рассмотрим работу водоструйного насоса (см. рис. 11). На подходе по нагнетательному трубопроводу 1 поток рабочей жидкости имеет относительно небольшую скорость v1 и высокое избыточное давление pизб1. Проходя через соплó 2, поток сужается, скорость его резко возрастает до v2. Для дальнейших рассуждений запишем уравнение Бернýлли так:
 .
.
Здесь нет z1 и z2, так как труба горизонтальная, а величиной потерь напора DH»0 пренебрегаем. Так как в правой части уравнения кинетическая составляющая энергии потока резко возросла из-за увеличения v2, то потенциальная составляющая, связанная с избыточным давлением после соплá pизб2, наоборот, уменьшится. Величину pизб2 можно выразить из этого уравнения и найти численное значение. Если pизб2 получается отрицательным, то, значит, возник вакуум (полное давление в струе стало меньше атмосферного). В последнем случае пьезометрическая линия опустится ниже отметки самой струи (см. рис 11).
Таким образом в струе рабочей жидкости после соплá образуется область пониженного давления или даже вакуум, что вызывает подсос транспортируемой жидкости по всасывающему трубопроводу 3 (см. рис. 11). Далее обе жидкости смешиваются в горловине 4 и транспортируются по отводящему трубопроводу 5.
Водоструйные насосы не имеют трущихся частей, в этом их преимущество перед механическими. По их принципу работают также эжекторы, гидроэлеваторы, насосы для создания вакуума.
Режимы движения жидкости
При проведении гидравлического расчёта в первую очередь нужно выяснять: какой режим движения будет наблюдаться у данного потока?
Режимы движения всех потоков (напорных и безнапорных) делятся на два типа (рис. 12):
1) ламинарный, то есть спокойный, параллельноструйный, при малых скоростях;
2) турбулентный, то есть бурлящий, вихреобразный, с водоворотами, при больших скоростях.
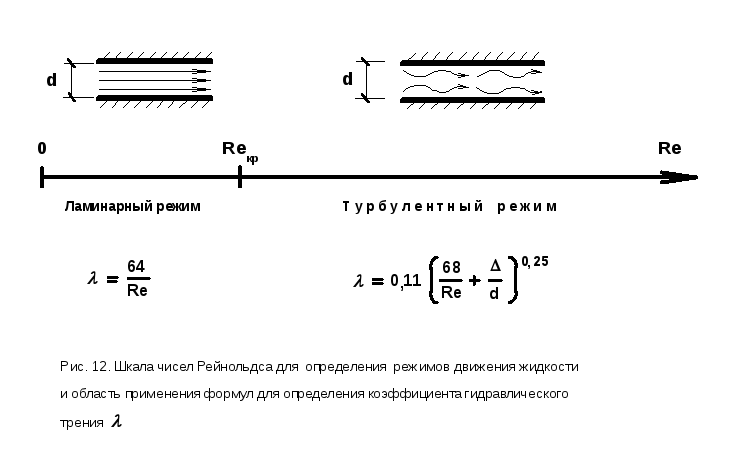
Для выяснения типа режима нужно рассчитать число Рейнольдса Re и сравнить его с критическим Reкр.
Число Рéйнольдса Re — это безразмерный критерий, вычисляемый по формулам:
— для напорных потоков
Re=vd/n,
где d- внутренний диаметр напорного трубопровода;
— для безнапорных потоков
Re=vR/n,
где R- гидравлический радиус безнапорного потока, м (см. с. 14).
Критическое число Рейнольдса Reкр — это число Рейнольдса, при котором наступает смена режима движения.
Для напорных потоков
Reкр=2320,
для безнапорных потоков
Reкр»500.
Упрощённо режим движения потока можно определить по шкале чисел Рейнольдса (см. рис. 12). Рассмотрим пример с напорной водопроводной трубой, у которой d=20мм, v=1м/с, n=10-6м2/с. Для потока в данной трубе число Рейнольдса составит:
Re=1×0,02/10-6 = 20000.
Число 20000больше, чем Reкр=2320 (для напорных потоков) и на рис.12 оно находится в правой части шкалы, следовательно, режим потока турбулентный и все дальнейшие гидравлические расчёты должны проводиться только по зависимостям и формулам для этого режима.
Источник