Какая сила давления действует на тело снизу

Сила Архимеда

Из опыта нам известно, что тело, находящееся в жидкости, весит меньше, чем, если оно находится в воздухе. Следовательно, на тело, погруженное в жидкость, действует выталкивающая сила. Величину этой силы определил ученый из древней Греции — Архимед.

Определение

Сила, с которой жидкость или газ действует на тело, погруженное в вещество, называют силой Архимеда (выталкивающей силой).

Данная сила появляется вследствие того, что давление жидкости (газа) увеличивается с ростом глубины. Получается, что сила давления, которая действует на тело со стороны жидкости (газа) снизу вверх больше, чем сила давления, направленная сверху вниз.

Закон Архимеда

Пусть тело в виде прямоугольного параллелепипеда полностью погрузили в жидкость рис.1. Будем считать, что верхнее и нижнее основания расположены горизонтально.

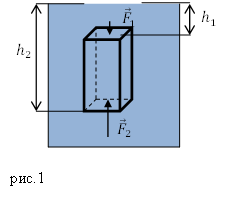
Силы, которые действуют на боковые грани параллелепипеда, уравновешиваются. Они лишь сжимают параллелепипед. Силы, действующие на верхнюю и нижнюю грани тела не равны между собой. Сила ($F_1$), с которой столб жидкости действует на верхнюю грань, равна:

[F_1=p_1S=rho gh_1S left(1right),]

где $rho $ — плотность жидкости; $S$ — площадь основания; $h_1$ — высота столба жидкости над верхним основанием параллелепипеда. Отметим, что давление атмосферы на жидкость мы не учитываем.

Величина силы, с которой жидкость действует на нижнее основание параллелепипеда, равна:

[F_2=p_2S=rho gh_2S left(2right),]

где $h_2$ — высота столба жидкости над нижним основанием. Так как $h_2>h_1$, значит $F_2>F_1$. Модуль равнодействующей силы, действующей на тело со стороны жидкости:

[F_A=F_2-F_1=rho g{S(h}_2-h_1) (3). ]

Если обозначить высоту параллелепипеда как $h=h_2-h_1$, тогда имеем:

[F_A=rho gSh=rho gV left(4right),]

где $V$ — объем параллелепипеда. Если тело находится в жидкости (газе) не целиком, то под V понимают объем находящийся в веществе (жидкости, газе). Правую часть выражения еще называют весом жидкости, которую вытесняет тело, погруженное в нее.

Сила Архимеда в жидкости и газе

На тело, находящееся в жидкости или газе, действует сила Архимеда, величина которой равна весу вещества (жидкости или газа) в объеме погруженной части тела. Сила Архимеда направлена вертикально вверх.

Данный закон выполняется для тел любой формы.

Сила Архимеда позволяет плавать лодкам и разного рода кораблям, несмотря на то, что плотность материала, из которого сделан корпус транспортного средства в несколько раз больше, чем плотность воды. Необходимо только чтобы вес воды, которую вытесняет подводная часть судна, был равен силе тяжести, которая действует на судно. Средняя же плотность корабля меньше плотности воды.

Сила Архимеда действует на тела находящиеся в воздухе. Но так как плотность воздуха мала, действием этой силы часто пренебрегают. В состоянии невесомости сила Архимеда равна нулю. В состоянии невесомости нет гидростатического давления.

Следует учесть, рассуждая о действии силы Архимеда, мы имеем в виду, что тело окружено жидкостью (газом), может быть за исключением своей верхней части. Если тело примыкаем ко дну сосуда или его стенке, то равнодействующая сил гидростатического давления станет прижимать тело ко дну или стенке. В этой связи, например, присасываются ко дну якоря кораблей, и если якорь лежит на большой глубине, то его крайне сложно оторвать от дна.

Примеры задач с силой Архимеда

Пример 1

Задание. Чему равно отношение силы трения ($F_{tr}$), которая действует на шарик, движущийся с постоянной скоростью вверх в жидкости, к силе тяжести ($mg$), если плотность жидкости (${rho }_g$) в $n$ раз больше плотности материала шарика (${rho }_{sh}$)?

Решение. Сделаем рисунок.

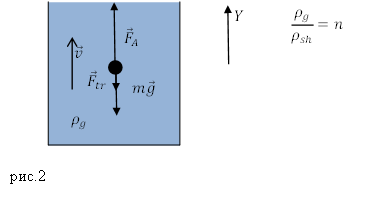
Запишем второй закон Ньютона для сил, действующих на шарик, учтем, что шарик всплывает равномерно, следовательно, его ускорение равно нулю:

[moverline{g}+{overline{F}}_A+{overline{F}}_{tr}=0 left(1.1right).]

В проекции на ось Y выражение (1.1) предстанет в виде:

[-mg-F_{tr}+F_A=0 left(1.2right).]

Модуль силы Архимеда найдем как:

[F_A={rho }_gVg left(1.3right).]

Сила тяжести, действующая на шарик:

[mg={rho }_{sh}Vg left(1.4right).]

Выразим из (1.2) силу трения, учтем выражения (1.3) и (1.4):

[F_{tr}=F_A-mg={rho }_gVg-{rho }_{sh}V left(1.5right).]

Найдем отношение $frac{F_{tr}}{mg}$:

[frac{F_{tr}}{mg}=frac{с_gVg-с_{sh}V}{с_{sh}Vg}=frac{с_g}{с_{sh}}-1=n-1.]

Ответ. $frac{F_{tr}}{mg}=n-1$

Пример 2

Задание. Сформулируйте условия плавания тел в жидкости. Что происходит с телом, если оно полностью погружено в жидкость, а плотность вещества тела равна плотности жидкости? Чему равна сила Архимеда, если тело плавает на границе раздела двух жидкостей с разными плотностями?

Решение. Из закона Архимеда можно легко получить условия плавания тел. Так, если сила Архимеда больше веса тела, то тело всплывает на поверхность жидкости до тех пор, пока не наступит равенства этих сил. Если сила Архимеда равна весу тела, то тело находится в состоянии покоя (плавает) в той точке жидкости, куда его поместили. Если сила Архимеда меньше веса тела, то тело тонет.

Если тело находится целиком в жидкости и плотности тела и жидкости равны, то тело плавает.

В случае если мы имеем несколько видов жидкостей с разными плотностями (например, поверх воды налили масло) и тело плавает на границе сред, то сила Архимеда будет равна:

[F_A=gleft[{rho }_1V_1+{rho }_2V_2right] left(2.1right),]

где ${rho }_1$ — плотность первой жидкости; ${rho }_2$ — плотность второй жидкости; $V_1$ — объем тела, находящийся в первой жидкости; $V_2$ — объем тела во второй жидкости.

Читать дальше: сила упругости.

Источник

Закон Архимеда. Условие плавания тел

Для того чтобы понять, что такое закон Архимеда, что такое выталкивающая сила Архимеда и откуда она берётся — необходимо знать, что такое гидростатическое давление жидкости, давление столба жидкости. С этими понятиями вы можете ознакомиться в предыдущей теме.

Гидростатическое давление жидкости имеет одно интересное свойство. Несмотря на то, что давление, в принципе, давит сверху на предмет, вдавливая предмет, который находится в жидкости, вниз — оказывается, что давление жидкости может и приподнимать предмет.

Рассмотрим подробнее, как именно жидкость давит на предмет, который в ней находится.

Для простоты возьмём в качестве предмета — кубик. На кубик будут действовать:

• давление сверху;
• давление с боков;
• давление снизу.

Как так получается, что, кроме давления сверху, на кубик действуют также давления сбоку и снизу? Почему?

«Дополнительные» давления будут присутствовать из-за гравитационного притяжения кубика и воды, которая его окружает.

Давления будут присутствовать из-за закона Паскаля, по которому давление в любой точке жидкости распространяется во все стороны.

Давления будут присутствовать из-за того, что кубик тонет.

Это утверждение неверно: на кубик, находящийся в воде, давление действует только сверху.

Как вы думаете, какое из давлений будет больше: на верхнюю грань или же на нижнюю?

На верхнюю грань, так как она выше — значит, и потенциальная энергия m g h mgh mgh больше

На нижнюю грань, так как она ниже — значит, глубина больше.

Давления одинаковы, так как они оба давят на один и тот же кубик.

Невозможно определить, какое из этих давлений больше, так как мы не знаем размеров кубика.

А что происходит с боковыми гранями кубика? Какое из давлений будет больше: справа или слева?

Давление справа будет больше.

Давление слева будет больше.

Давления справа и слева будут равны друг другу.

Однозначно сказать нельзя, надо знать плотность жидкости и плотность кубика.

Получается, «боковые» давления никак не двигают кубик, а вот давление снизу «подталкивает» кубик вверх и при этом «побеждает» давление сверху, поскольку давление сверху меньше, чем давление снизу. Получается, что жидкость выталкивает кубик. Выталкивает с некоторым давлением — а значит, применяет к кубику некоторую выталкивающую силу. Чтобы найти эту силу, попробуем подсчитать, насколько давление снизу будет больше, чем давление сверху, насколько нижнее давление сильнее «выталкивает» кубик, чем верхнее — «вталкивает».

Сначала найдем разность давлений на верхнюю и нижнюю грани кубика:

p 4 − p 1 = ρ ж и д к о с т и g h 4 − ρ ж и д к о с т и g h 1 = p_4 — p_1 = rho_{жидкости} gh_4 — rho_{жидкости} gh_1 = p4​−p1​=ρжидкости​gh4​−ρжидкости​gh2​=

= ρ ж и д к о с т и g ( h 4 − h 1 ) = rho_{жидкости} g (h_4 — h_1) =ρжидкости​g(h4​−h2​).

Из рисунка видно, что разница между h 4 h_4 h4​ и h 1 h_1 h2​ — это не что иное, как высота кубика, то есть h h h. Значит, формулу разности давлений можно записать в следующем виде:

p 4 − p 1 = ρ ж и д к о с т и g ( h 4 − h 1 ) = ρ ж и д к о с т и g h p_4 — p_1 = rho_{жидкости} g (h_4 — h_1)= rho_{жидкости} gh p4​−p1​=ρжидкости​g(h4​−h2​)=ρжидкости​gh.

Найдем теперь не выталкивающее давление, а выталкивающую силу. Давайте вспомним, как связаны сила и давление.

Как связаны сила F F F с давлением p p p, если площадь, на которую действует сила, равна S S S? Выберите верное равенство.

F = p F = p F=p

p = F S p = frac{F}{S} p=SF​

p = F ⋅ S p = F cdot S p=F⋅S

p ⋅ F = S p cdot F = S p⋅F=S

Тогда формула для выталкивающей силы:

F = p ⋅ S = ( p 4 − p 1 ) ⋅ S = ρ ж и д к о с т и g h ⋅ S F = p cdot S = (p_4 — p_1) cdot S = rho_{жидкости} gh cdot S F=p⋅S=(p4​−p1​)⋅S=ρжидкости​gh⋅S.

Как можно упростить это выражение?

Можно убрать ускорение свободного падения g g g, так как всё происходит внутри жидкости.

Можно заменить произведение плотности ρ ж и д к о с т и rho_{жидкости} ρжидкости​ и площади S S S на силу F F F — есть такая формула.

Можно заменить произведение высоты h h h и площади S S S на объём тела.

Можно использовать безвременную формулу из кинематики 2 a ⋅ S = V 2 − V 0 2 2a cdot S = V^2 — V_0^2 2a⋅S=V2−V02​, подставив вместо ускорения a a a ускорение свободного падения g g g.

Выталкивающую силу называют силой Архимеда, а её формулу, которую мы только что вывели, — законом Архимеда:

F А р х и м е д а = ρ ж и д к о с т и g V т е л а F_{Архимеда} = rho_{жидкости} gV_{тела} FАрхимеда​=ρжидкости​gVтела​

Обратите внимание на то, от каких величин зависит сила Архимеда.

1. От плотности жидкости. Чем плотнее жидкость, тем сильнее она будет выталкивать тело. Поэтому, например, в солёной морской воде плавать легче, чем в пресной речной.

2. От ускорения свободного падения. Фактически — от того, насколько сильно Земля притягивает. Можно сделать вывод, что на других планетах сила Архимеда будет другой — потому что там у ускорения свободного падения другие значения.

3. От объёма тела. Чем больше объём тела, тем сильнее его выталкивает жидкость. Вспомните, как легко удержать под водой маленький мячик (например, мячик для игры в настольный теннис) и как сложно сделать то же самое с большим надувным мячом для игр на пляже.

Закон Архимеда справедлив для тела любой формы — не только кубика. И в формуле будет использоваться объем погруженного тела.

В формуле фигурирует не объём всего тела, а только той его части, что погружена в воду.

То есть, если какая-то часть тела «выглядывает» из воды — она в формуле закона Архимеда не участвует.

Условие плавания тел

Как мы с вами поняли — сила Архимеда действует на все тела, которые погружены в жидкость. Тогда все тела должны из жидкости выталкиваться и всплывать. Почему же этого не происходит — и некоторые тела плавают, а некоторые — тонут?

Почему некоторые тела тонут (небольшая подсказка: рассмотрите, какие ещё силы действуют на тело в воде)?

Закон Архимеда не всегда справедлив; есть случаи, когда он не работает.

На некоторые вещества (некоторые материалы) сила Архимеда не действует.

Плавание/неплавание тел зависит от силы тяжести, которая действует на тело.

На всё воля Высшего Разума — может, будет плавать, может — нет.

Тело плавает, если:

F А р х и м е д а ≥ m т е л а g ⇔ ρ ж и д к о с т и g V т е л а ≥ m т е л а g ⇔ F_{Архимеда} ge m_{тела}g Leftrightarrow rho_{жидкости} gV_{тела} ge m_{тела} g Leftrightarrow FАрхимеда​≥mтела​g⇔ρжидкости​gVтела​≥mтела​g⇔

⇔ ρ ж и д к о с т и V т е л а ≥ m т е л а Leftrightarrowrho_{жидкости} V_{тела} ge m_{тела} ⇔ρжидкости​Vтела​≥mтела​.

Массу тела можно расписать через плотность тела и объем тела:

ρ ж и д к о с т и V т е л а ≥ m т е л а ⇔ ρ ж и д к о с т и V т е л а ≥ ρ т е л а V т е л а ⇔ rho_{жидкости} V_{тела} ge m_{тела}Leftrightarrow rho_{жидкости} V_{тела} ge rho_{тела} V_{тела} Leftrightarrow ρжидкости​Vтела​≥mтела​⇔ρжидкости​Vтела​≥ρтела​Vтела​⇔

⇔ ρ ж и д к о с т и ≥ ρ т е л а Leftrightarrow rho_{жидкости} ge rho_{тела} ⇔ρжидкости​≥ρтела​.

Мы получили очень важный вывод! Тело плавает в жидкости тогда, когда плотность тела оказывается меньше плотности жидкости.

Именно по этой причине два одинаковых по объёму тела в воде могут вести себя по-разному: небольшой камешек утонет, а рыбацкий поплавок примерно такого же объёма — будет плавать.

Условие плавания тел: ρ ж и д к о с т и ≥ ρ т е л а rho_{жидкости} ge rho_{тела} ρжидкости​≥ρтела​

В воде находятся три шарика одинаковой массы, удерживаемые нитями (см. рисунок).





При этом

архимедова сила, действующая на первый шарик, направлена вниз, а на второй и третий — вверх.

на первый шарик действует наибольшая архимедова сила.

на все шарики действуют одинаковые архимедовы силы, так как их массы равны.

на третий шарик действует наибольшая архимедова сила.

Разберем более сложную задачу.

Условие

На границе раздела двух несмешивающихся жидкостей, имеющий плотности ρ 1 = 9 0 0 к г / м 3 rho_1 = 900text{ }кг/м^3 ρ1​=900 кг/м3 и ρ 2 = 3 ρ 1 rho_2 = 3rho_1 ρ2​=3ρ1​, плавает шарик (см. рисунок). Какова должна быть плотность шарика ρ rho ρ, чтобы выше границы раздела жидкостей была одна треть его объёма? Ответ выразите в к г / м 3 кг/м^3 кг/м3.

(Источник: ЕГЭ-2015. Физика. Демо-версия)

Решение

Шаг 1. Определим, какие силы действуют на шарик.

Выберите все силы, которые действуют на шарик.

сила тяжести

сила Архимеда со стороны первой жидкости

сила Архимеда со стороны второй жидкости

сила реакции опоры

сила трения

сила упругости

Шаг 2. Попробуем нарисовать то, как направлены все три силы.

Сделайте рисунок и сравните с нашим.

Шаг 3. Попробуем связать эти три силы: силу тяжести, силу Архимеда со стороны первой жидкости и силу Архимеда со стороны второй жидкости.

Как вы думаете, как связаны эти три силы? Составьте формулу.

Составьте правильную формулу.

Шаг 4. Выразим силы Архимеда и силу тяжести через другие величины.

Перепишем равенство F А р х и м е д а 1 + F А р х и м е д а 2 = m g F_{Архимеда_1}+F_{Архимеда_2}=mg FАрхимеда1​​+FАрхимеда2​​=mg. Выберите верное выражение.

ρ ж и д к о с т и 1 g V 1 + ρ ж и д к о с т и 2 g V 2 = ρ т е л а g V 1 + 2 rho_{жидкости_1}gV_1 + rho_{жидкости_2}gV_2 = rho_{тела}gV_{1+2} ρжидкости1​​gV1​+ρжидкости2​​gV2​=ρтела​gV1+2​

ρ ж и д к о с т и 1 g V 1 = ρ т е л а g V 1 + 2 rho_{жидкости_1}gV_1 = rho_{тела}gV_{1+2} ρжидкости1​​gV1​=ρтела​gV1+2​

ρ ж и д к о с т и 2 g V 2 = ρ т е л а g V 1 + 2 rho_{жидкости_2}gV_2 = rho_{тела}gV_{1+2} ρжидкости2​​gV2​=ρтела​gV1+2​

ρ ж и д к о с т и 2 g V 1 + ρ ж и д к о с т и 1 g V 2 = ρ т е л а g V 1 + 2 rho_{жидкости_2}gV_1 + rho_{жидкости_1}gV_2 = rho_{тела}gV_{1+2} ρжидкости2​​gV1​+ρжидкости1​​gV2​=ρтела​gV1+2​

Шаг 5. Выполним некоторые преобразования и подставим значения из условия задачи.

Сократим ускорение свободного падения: ρ ж и д к о с т и 1 V 1 + ρ ж и д к о с т и 2 V 2 = ρ т е л а V 1 + 2 rho_{жидкости_1}V_1 + rho_{жидкости_2}V_2 = rho_{тела}V_{1+2} ρжидкости1​​V1​+ρжидкости2​​V2​=ρтела​V1+2​.

Подставим плотности жидкостей: ρ ж и д к о с т и 1 V 1 + 3 ⋅ ρ ж и д к о с т и 1 V 2 = ρ т е л а V 1 + 2 rho_{жидкости_1}V_1 + 3 cdot rho_{жидкости_1}V_2 = rho_{тела}V_{1+2} ρжидкости1​​V1​+3⋅ρжидкости1​​V2​=ρтела​V1+2​.

Учтём, что по условию задачи: V 1 = 1 3 V т е л а V_1 = frac{1}{3}V_{тела} V1​=31​Vтела​, V 2 = 2 3 V т е л а V_2 = frac{2}{3}V_{тела} V2​=32​Vтела​. Отсюда ρ ж и д к о с т и 1 1 3 V т е л а + 3 ⋅ ρ ж и д к о с т и 1 2 3 V т е л а = ρ т е л а V т е л а rho_{жидкости_1} frac{1}{3}V_{тела} + 3 cdot rho_{жидкости_1} frac{2}{3}V_{тела} = rho_{тела}V_{тела} ρжидкости1​​31​Vтела​+3⋅ρжидкости1​​32​Vтела​=ρтела​Vтела​.

Сократим объём тела: ρ ж и д к о с т и 1 1 3 + 3 ⋅ ρ ж и д к о с т и 1 2 3 = ρ т е л а rho_{жидкости_1} frac{1}{3} + 3 cdot rho_{жидкости_1} frac{2}{3} = rho_{тела} ρжидкости1​​31​+3⋅ρжидкости1​​32​=ρтела​.

Выполним суммирование в левой части: 7 3 ⋅ ρ ж и д к о с т и 1 = ρ т е л а frac{7}{3} cdot rho_{жидкости_1} = rho_{тела} 37​⋅ρжидкости1​​=ρтела​.

Поменяем левую и правую части местами и подставим в выражение значение плотности первой жидкости: ρ т е л а = 7 3 ⋅ 9 0 0 к г / м 3 = 2 1 0 0 к г / м 3 rho_{тела} = frac{7}{3} cdot 900 кг/м^3 = 2100 кг/м^3 ρтела​=37​⋅900кг/м3=2100кг/м3.

Ответ. ρ т е л а = 2 1 0 0 к г / м 3 rho_{тела} = 2100 кг/м^3 ρтела​=2100кг/м3.

Задачи для самостоятельного решения: #закон архимеда

Источник